 With new TEKS in tow, my 7th graders taking 8th grade math have been studying proportional and non-proportional linear relationships (wow, right?). The progression has been a refreshing, concept-based study of LOTS of scenarios featuring “constant rates of change” represented in tables and with graphs, making clear connections to the similar triangles we studied in our last unit (Thank you Desmos for this beautiful contribution! Twitter can be SO POWERFUL in sharing resources, and I thank Desmos for entertaining my request by sharing this beauty!) We didn’t even use the word “slope” until about day 3 of our learning when we introduced the traditional subscript-laden formula. They didn’t flinch once they saw that the formula was simply showing what we’ve been doing all along, and the word “slope” became a lot less scary.
With new TEKS in tow, my 7th graders taking 8th grade math have been studying proportional and non-proportional linear relationships (wow, right?). The progression has been a refreshing, concept-based study of LOTS of scenarios featuring “constant rates of change” represented in tables and with graphs, making clear connections to the similar triangles we studied in our last unit (Thank you Desmos for this beautiful contribution! Twitter can be SO POWERFUL in sharing resources, and I thank Desmos for entertaining my request by sharing this beauty!) We didn’t even use the word “slope” until about day 3 of our learning when we introduced the traditional subscript-laden formula. They didn’t flinch once they saw that the formula was simply showing what we’ve been doing all along, and the word “slope” became a lot less scary.
The next step was to add equations to the mix of representations. Though the text introduces proportional linear first (think direct variation… or y = mx + 0… or y = kx), I mixed things up and started with non-proportional linear (think y = mx + b). That way, I could emphasize that “b” was just zero in the proportional flavor.
After some scenarios, we talked about how to find an equation if we weren’t given one. Is it possible to write an equation of a line if all we know about the line is that it passes through two specific points?
 I created this “chunking activity” to help students think through the steps. If we want an equation in slope-intercept form, it would be helpful to have the slope (we can find that) and the y-intercept (we can find that too). After writing each equation in slope-intercept form, we used Y = on our TI graphing calculators to enter the equation, view the table, and confirm that our line passed through the two points we started with. After guiding students through the process, they had a few equations to muster up for homework.
I created this “chunking activity” to help students think through the steps. If we want an equation in slope-intercept form, it would be helpful to have the slope (we can find that) and the y-intercept (we can find that too). After writing each equation in slope-intercept form, we used Y = on our TI graphing calculators to enter the equation, view the table, and confirm that our line passed through the two points we started with. After guiding students through the process, they had a few equations to muster up for homework.
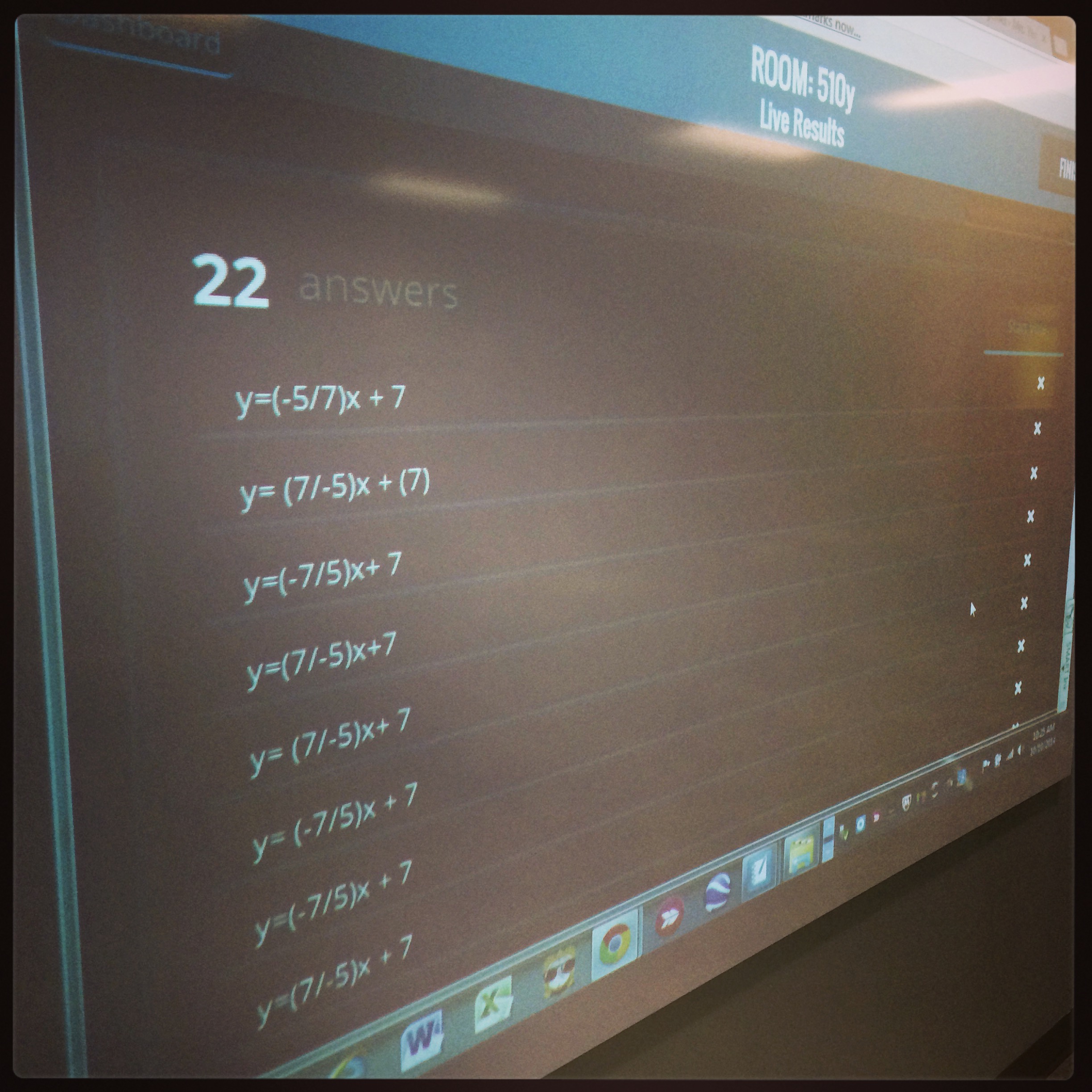
 The next day, I used Socrative to review homework. On the fly, I selected “Quick Question” then “Short Answer” and asked students to enter their first equation. Using Socrative to type in equations reinforced the keystrokes needed to enter an equation in the TI using the Y = key. Anonymous equations appeared in a list at the front of the class, and conversations about discrepancies began.
The next day, I used Socrative to review homework. On the fly, I selected “Quick Question” then “Short Answer” and asked students to enter their first equation. Using Socrative to type in equations reinforced the keystrokes needed to enter an equation in the TI using the Y = key. Anonymous equations appeared in a list at the front of the class, and conversations about discrepancies began.
Is the slope -7/5 the same as 7/-5? How about -7/-5? What do the folks who represented the slope as -5/7 instead need to know? Sure, Socrative doesn’t have a “pretty” equation editor, but discussions about the meaning of (-7/5)x versus -7/5x versus -7/(5x) might not have happened without the wonky-looking representations.
Graphing lines
y = (-7/5)x
y = -7/5x and
y = -7/(5x)
simultaneously to test parentheses placements added a level of richness to this simple, initially skill-based task. We entered each equation from the homework, one at a time, using the same process in Socrative, viewing the anonymous list and continuing the conversation. By the third or fourth equation, we had a nearly unanimous list of slope-intercept form equations, as students had learned and made adjustments to their equations stemming from our discussions along the way.
I can’t overstate the impact that making student thinking visible using simple, free tech tools like Socrative can have on student discourse.
How are you using Socrative in the classroom?
















From a differentiation standpoint, if you’re using the Socrative “Teacher Paced Tool,” what do you do for students who know the answer right away, versus students who take a long time to solve it?
Hi Danielle!
Generally, I used “Teacher Paced” for math that is less-involved, such as looking for patterns with exponents. This way, there is less of a timing issue as you suggest. Additionally, Socrative “Teacher Paced” could be used for answer entry for an assignment that was completed previously. That way, the math is done ahead of time, and Socrative is used to present student data swiftly for instructional decision-making and student discussion. I hope that helps!
It does, thanks! I really want to start using technology more to get immediate feedback, however as I mentioned I struggle doing activities like that as I have many students that are struggling, mixed with many that don’t speak English, mixed with some over-achievers! As a whole it is an awesome classroom environment for collaboration, but I struggle with individual activities to give immediate feedback.