The title of this post is an idea that I think about several times a week while I’m teaching and planning. Maybe you’ve been there.
~ You’re solving proportions and a kiddo with stars in her eyes exclaims, “The BUTTERFLY METHOD!”
~ You’re isolating a variable while solving equations, and when you ask what’s next, a student offers, “Well, those cancel out, so you have x = -3…”
~ You’re solving inequalities in one variable, and as you graph the solutions on a number line, an excited student exclaims, “I know a shortcut! The way the symbol is pointing tells you which way to point the arrow when you graph it!”
Some of these “a-ha” moments might happen as we’re teaching (the inequality idea above, for example). I have no data to back this up, but my guess is that more often than not, these ideas have been explicitly taught to students by well-intentioned teachers and tutors. Yet, when students are asked to think differently… well… a recent tweet from Jonathan Osters comes to mind…
My students when I ask them to do a problem slightly different from the one we just did 😉 #iteachmath pic.twitter.com/Z7JPE4LkYe
— Jonathan Osters (@callmejosters) November 20, 2017
When these moments inevitably happen in your classroom, literally, what is your next move? What’s the expression on your face looking like? What are the words that you say? What’s next?
I have handled these moments across the gamut – with grace, all the way down to (sporting my best pouty face), “I never use the word cancel… except when I tell students that I never use the word cancel.”
How do we respect those who are trying to help students by teaching them “tricks”, yet steer things toward learning mathematics for understanding (especially when students LOVE and ADORE a good trick)? Simply asking and pursuing, “Why does that work?” can help – some students’ reactions are PRICELESS as I watch them UNDERSTAND the mathematics right before my eyes. Other students look a bit like Osters’ aforementioned tweet, preferring the “trick” that “works” instead.
I’ve gotten lots of ideas for exploring alternatives that promote understanding from Nix the Tricks. If they’re already pre-programmed to “FOIL” I’ve found the conversation about why that acronym is so silly (because it only helps when multiplying two binomials) can bring clarity.
Another approach I’ve tried is to create “proactive problems” and ask strategic questions as we work them. I see huge potential in creating some sort of problems-resource as a community that might help us be more proactive in the moments before a student is just about to utter the “trick”.
~ Instead of cross-products right out of the gate, ask students, “How can we isolate the variable in this equation?” (What? Proportions are equations?!? I can multiply both sides of the equation by 40 first? I can DO that?)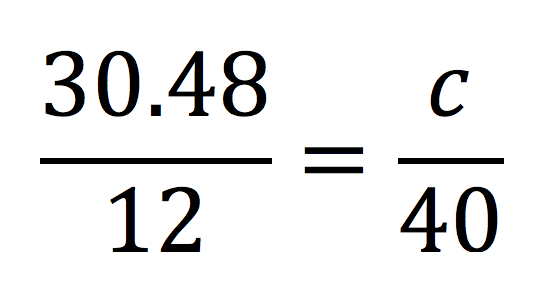
~ Instead of saying “cancel” during instruction, verbally describe what’s happening every time using visuals and concepts of identities. Reinforce this language as students begin to use it when they explain their thinking.
What are your favorite ways of handling “tricky” instructional moments of opportunity?
And, I’d be naive to think there aren’t things that *I* am explicitly teaching my students, with the best of intentions, that might drive my students’ future math teachers nuts.
What topics and methods am *I* teaching right now that will make my students’ future math teachers roll their eyes?
What sort of “proactive problems” handed down from my students’ future math teachers could also help ME know why I might consider changing the way I present certain topics now?
How can we get better at this?
Follow-up: Check out Dan Meyer’s living document of ideas from folks all over to help create “Mathematical Headaches”
Might we create a similar resource along the lines of… “Rethinking Tricks with Proactive Problems” Directory? or “Instructional Language to Overcome Tricks” Directory?















