I’m back in the groove with a fantastic new-to-me crew of learners, spending short snippets of time on Twitter… and neglecting to blog! It’s time to hammer down several threads that resonated with me and recent experiences with my own students in this mash-up post.
Knowing Order of Operations would be part of my own review with students, and likely a topic in many mathy classrooms, I shared “Twin Puzzles”.
I’d bet many of us are reviewing “Order of Operations” soon! Looking for a different way to challenge students? Check out this @Desmos activity: Twin Puzzles! https://t.co/goAbOTZm9N #iteachmath #MTBoS
— Cathy Yenca (@mathycathy) August 25, 2018
I also shared another strategy to address Order of Operations – combining the famous Four Fours with Nearpod to capture and share students’ favorite equations that they believed no other student had come up with in our class.
(1) Assigned “The Four Fours” for HW yesterday. (2) Today, heard stories about how Ss’ families got involved in the fun! (3) Created a @nearpod in less than a minute. (4) Virtually sent every S to the board with “Draw It”! (5) Showcased every S’s thinking!https://t.co/H2FcnPyXJ3
— Cathy Yenca (@mathycathy) August 31, 2018
Then, I caught this problem (both the math problem and the problem with the way a teacher seemingly used this math problem as a gotcha, causing students to second-guess their own math ability, making for a rocky start…)
I have a dilemma and I need your help having a difficult, but critical conversation with a teacher I don’t know. #MTBoS #iteachmath #mathchat https://t.co/5LC5m242tQ
— chase orton (@mathgeek76) September 4, 2018
And… this plea that there is no excuse to mention Aunt Sally… please!
Hey #MSMath teachers, please don’t teach your students PEMDAS, it’s really misleading. They see 6 letters and think there are 6 steps. Thanks!
— Nick Corley (@MrCorleyMath) September 8, 2018
Additionally, Dan Meyer’s recent blog post and thread on Twitter seems to speak to all of our Order of Operations discussions.
What does a student look like in your class who has procedural fluency but lacks conceptual understanding? Three from me. More from you. #iteachmath #fluencyisnotenough https://t.co/r9Viwl66no
— Dan Meyer (@ddmeyer) September 5, 2018
Whether you call it PEMDAS, GEMS, Order of Operations, or something else, the Order-of-Things procedure becomes extremely mushy to students… even though the “rules” don’t change, the problems do.
What have students looked like in my class who possess procedural fluency but lack conceptual understanding?
Students perceive these problems as being “wrong” because “multiplication comes before division” and “addition comes before subtraction”.
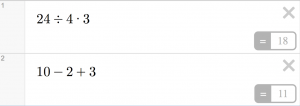
Students stop dead in their tracks at this problem, wrestling with their knowledge of number properties, and whether to distribute the 4, or subtract 5 – 7 first.
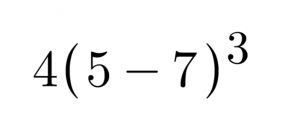
Students ask, “How do I know whether I should distribute first or follow the correct order of operations?” for a numerical expression like this, without realizing that BOTH methods lead to the same, correct answer, OR, that distributing first might lighten the load.
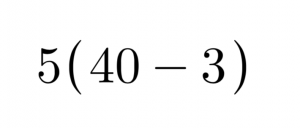
(Note: I created this activity with this premise in mind – that students don’t generally realize the result will be the same either way, or how to decide when distributing might be more efficient, and when Order of Operations might be more efficient.)
Students insist on doing the “grouping symbols” first in a problem like this, even though the parentheses only contain a single value.
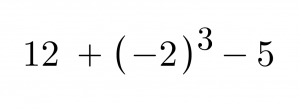
Is it our use of mnemonics like PEMDAS or GEMS that have contributed to students’ confusion? Is the solution to add context to these “naked problems”? Do MORE problems, so that more exposure to lots of problems helps bring clarity? I appreciated these questions on Twitter as well… as teachers sometimes we know what we SHOULDN’T do, but we’re not sure what TO do, especially when students have similar misunderstandings year… after year… after year.
What’s the alternative? Not trying to be combative, genuinely asking.
— Brian Ball (@MrBallMath) September 8, 2018
How would you introduce GEMA to s/s who are encountering order of operations for the 1st time? (Also not being combative, definitely genuinely interested!)
— LC Dawson (@CDawson18) September 9, 2018
And a final thought: Every misconception and question students ask that reveals some level of procedural understanding without conceptual understanding is a learning opportunity. What THEY do next and what WE do next matters too! There’s no formula for how to handle these “teachable moments” with our own students. However, fostering a classroom culture that values questioning, mistakes, and exploring multiple methods flexibly and respectfully is a great start.
Interesting thread! Important thing to consider regarding examples shared here is what a S does NEXT. ie. After doing a procedure without considering the concept initially, does the S now experience an A-HA? If so, we’ve crossed the procedure/concept line. WIN! #iteachmath #MTBoS https://t.co/5DUahrkQzk
— Cathy Yenca (@mathycathy) September 8, 2018
Speaking of great starts, I hope your year is off to one!
And, if you want to explore many, many, many perspectives on fluency versus conceptual understanding, you’re in for a ton of food-for-thought here.
UPDATE: And… folks are still discussing…!
Teach the controversy. https://t.co/Fu8BKZ6y6e
— Dan Meyer (@ddmeyer) September 11, 2018















