JUST KIDDING! That catchy title doesn’t begin to give justice to the hard-working colleagues I have the pleasure of planning with… the ones in my PLCs locally, AND the global ones who have been sharing about their experiences to help all of us be better.
I am BY NO MEANS posting ANY of this to say “Here’s How To Be an Online Teacher”… this is me saying, this is what I have tried in my 2-whole-days of experience, mostly because I’d love to know how YOU are doing this, and how I can do a better job because you’ve already learned or realized something that I’m not yet seeing.
Okay, my tongue-in-cheek post begins now.
Step 1: PLC Planning
PLC with teammates via ZOOM, e-mail, and/or texting at all hours. Calm each other down when technology behaves questionably. Share resources so we can all survive. Document all lesson plans in a concise report (see mine below… HAHAHAHAHA)
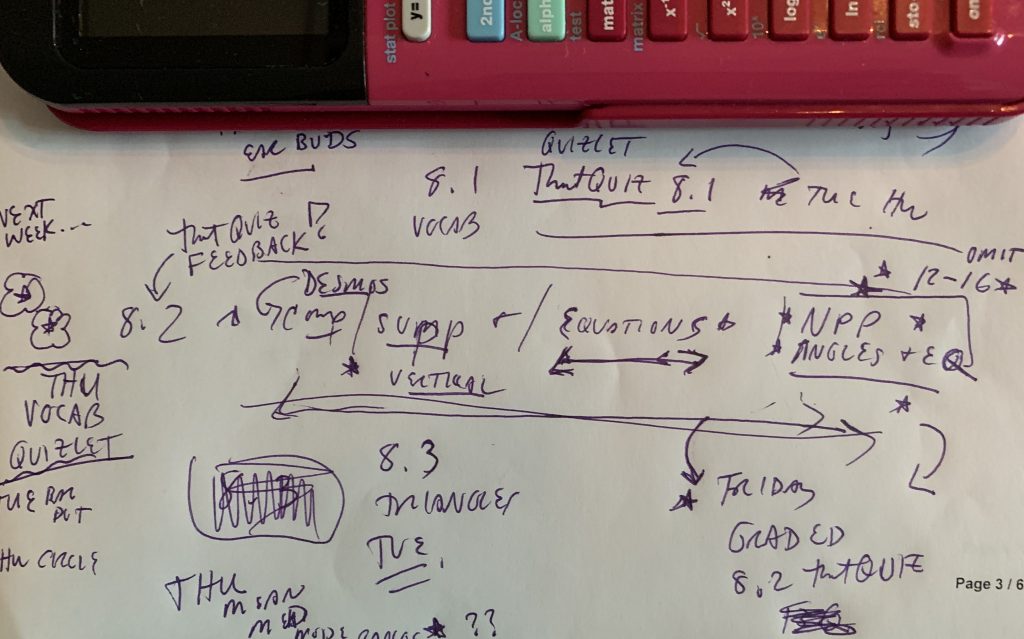
Step 2: Consolidate the Plans
Interpret chicken-scratch and transfer to index cards, labeled by day/class period. Realize the resources listed actually need to be located… find, create, and/or share needed resources* {see more about resources at the end of this post}. Brew a cup of coffee. Brew another.

Step 3: Digitize
Transfer index-card ideas to Numbers spreadsheet. Include links to aforementioned resources. (This process digitizes my plans, and helps me think about how to also rewrite my teacher-plans into student-friendly plans to be posted for them later…)
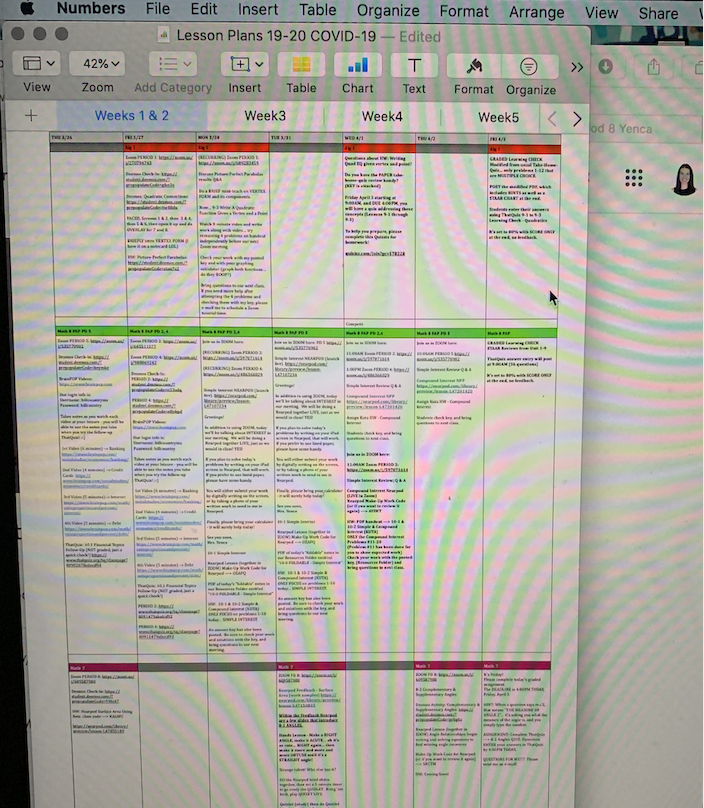
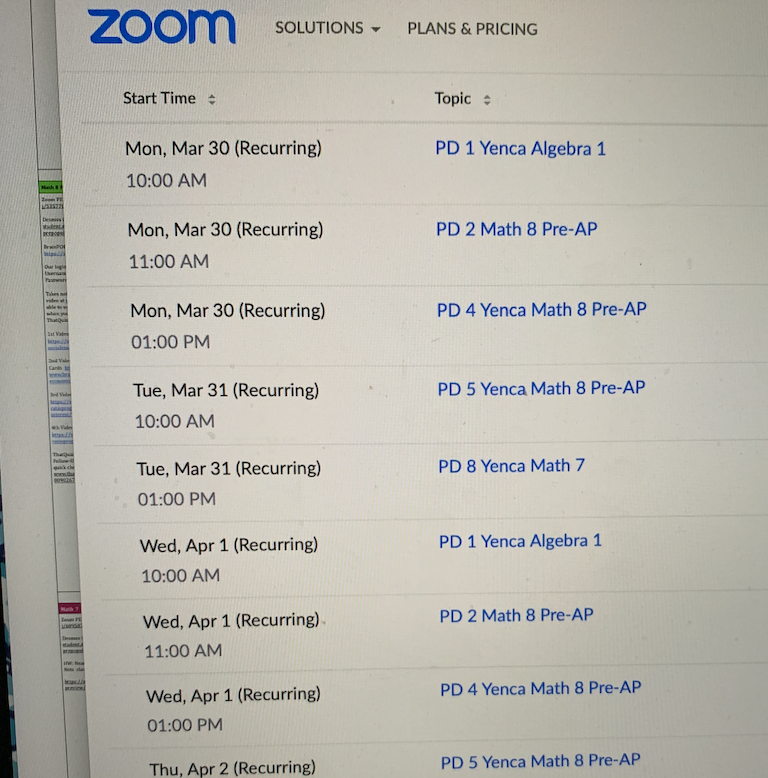
Step 4: Zoom
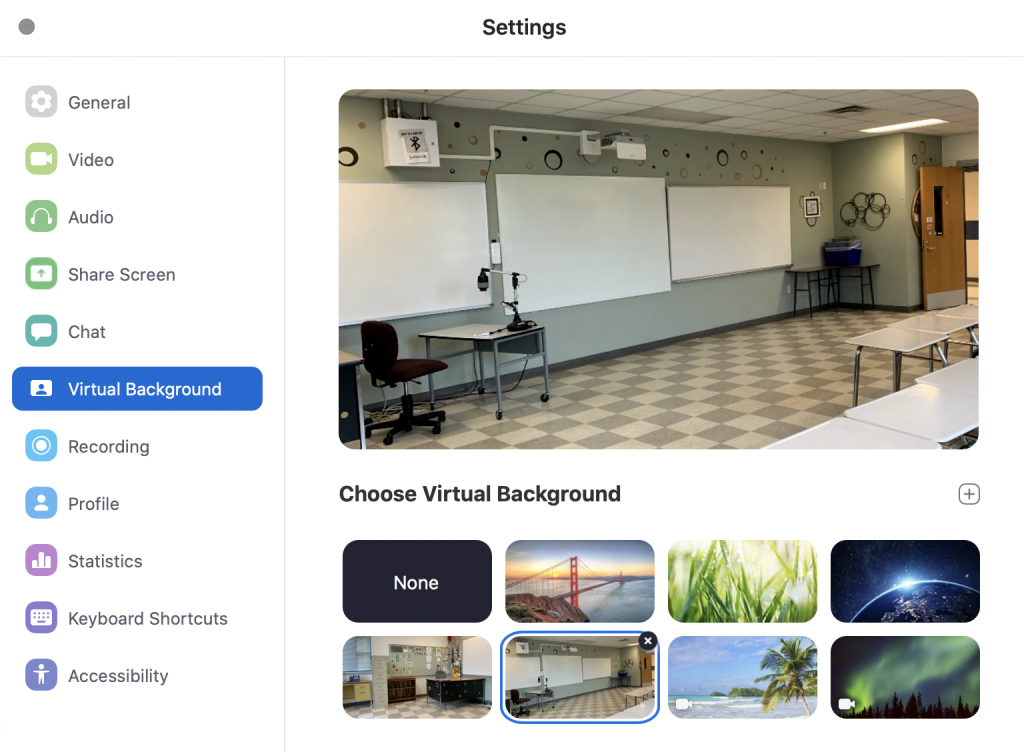
Set up Zoom meetings for each class, being mindful of all settings. Use a photo of my classroom as the virtual background for a personal touch!
Step 5: Rearrange the Furniture in Your Home
Realize that a Zoom Virtual Background does not stop household noises or the flow of humans through the open dining room. Rearrange the dining room and bedroom furniture. Ensure every worker-and learner-from-home has his/her own room… with a DOOR.

Step 6: Schedule
Close the bedroom door. Copy-and-paste student-friendly, digital post from Numbers spreadsheet into Google Classroom for each pertinent class (I teach three different courses), remembering to create unique links for each activity for each class for each day, including details for accessing each Zoom meeting. (Each time a class meets, I’ve been plopping everything into one announcement in GC and scheduling it ahead of time to post 30-minutes before each scheduled Zoom meeting.)
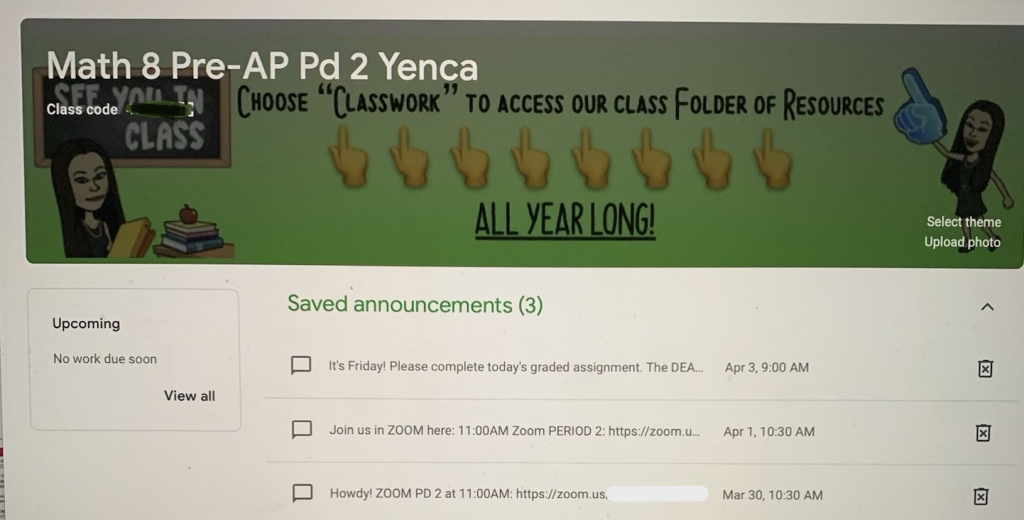
Step 7: Post Agenda
Post a concise agenda-version of Google Classroom student-post on Google Calendar for parents to access and view.
Step 8: MEET WITH THE KIDS!
Watch Google Classroom post your announcement at the scheduled time… and launch the Zoom Meeting (anyone else get butterflies in their stomachs when they do this the first few times?!? I was as nervous as the first day of school, pressing that button!)
Rinse and repeat from now until the unknown end of all of this…!
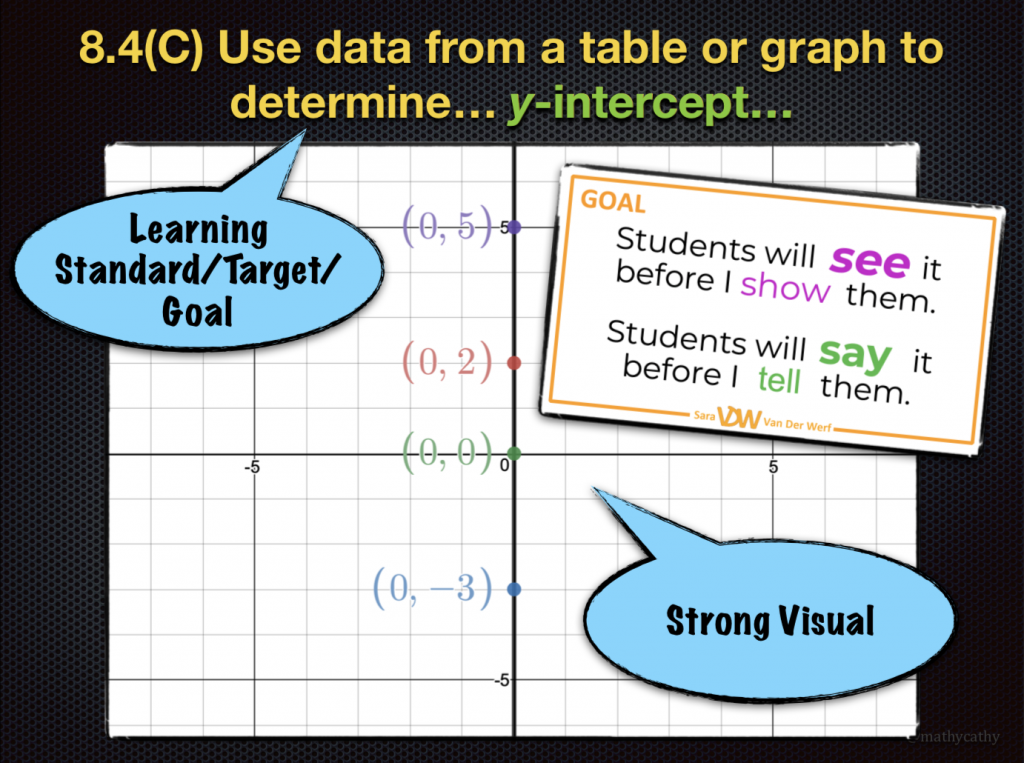
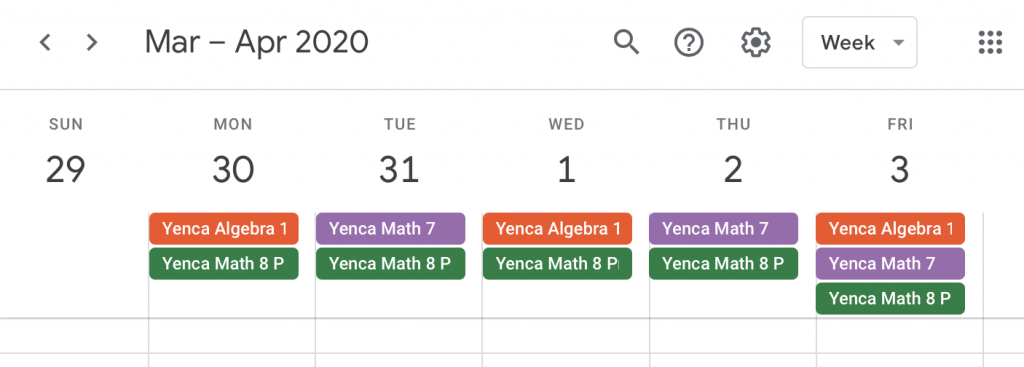
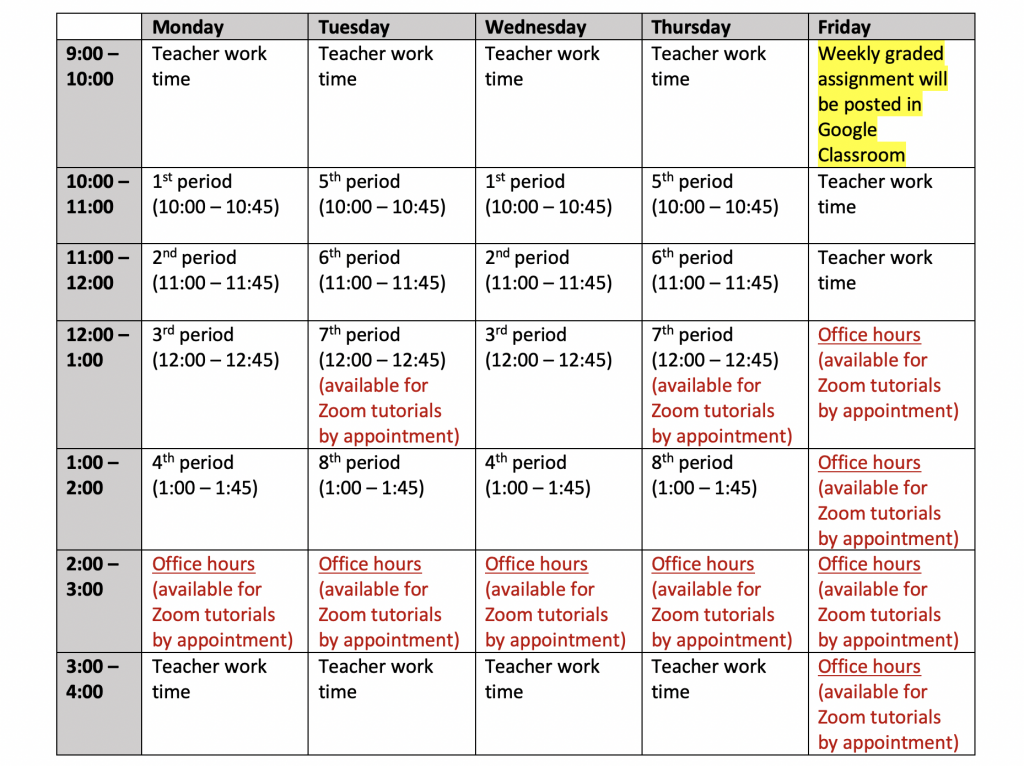
For reference, here’s what my schedule will look like each week! A MILLION THANKS to my colleague Georgia for helping our entire department take a more general schedule and streamline it purposefully to this! 🙂
This planning process has honestly felt like I am creating never-ending sub plans, because of the level of detail needed to ensure that we maximize our Zoom time together, that we present concepts using what we perceive to be the best tools within our realm of familiarity to meet the objective(s) at hand… it really is A LOT.
NOT COMPLAINING, just the facts!
As a matter of fact, I couldn’t be more grateful to be safely grounded at home with two of my favorite humans, while also having the opportunity to continue to teach and connect with my students through a schedule that has been thoughtfully set up by amazing district leadership. We can keep on moving and shaking with curriculum, while adjusting expectations and demands.
Step 9: Just Breathe
Eat something. Drink water. WASH THOSE HANDS. Get away from the screen. Go outside and breathe the fresh air. Stop hitting “refresh” and looking at that COVID map for a bit (I’m talking to myself here!) Exercise. Take a walk. Chat with friends and family. Don’t try to do it all right now… (Also, talking to myself…!)
Okay, GO! Tell me of the magical ways you’ve streamlined your planning while not sacrificing quality in the process!
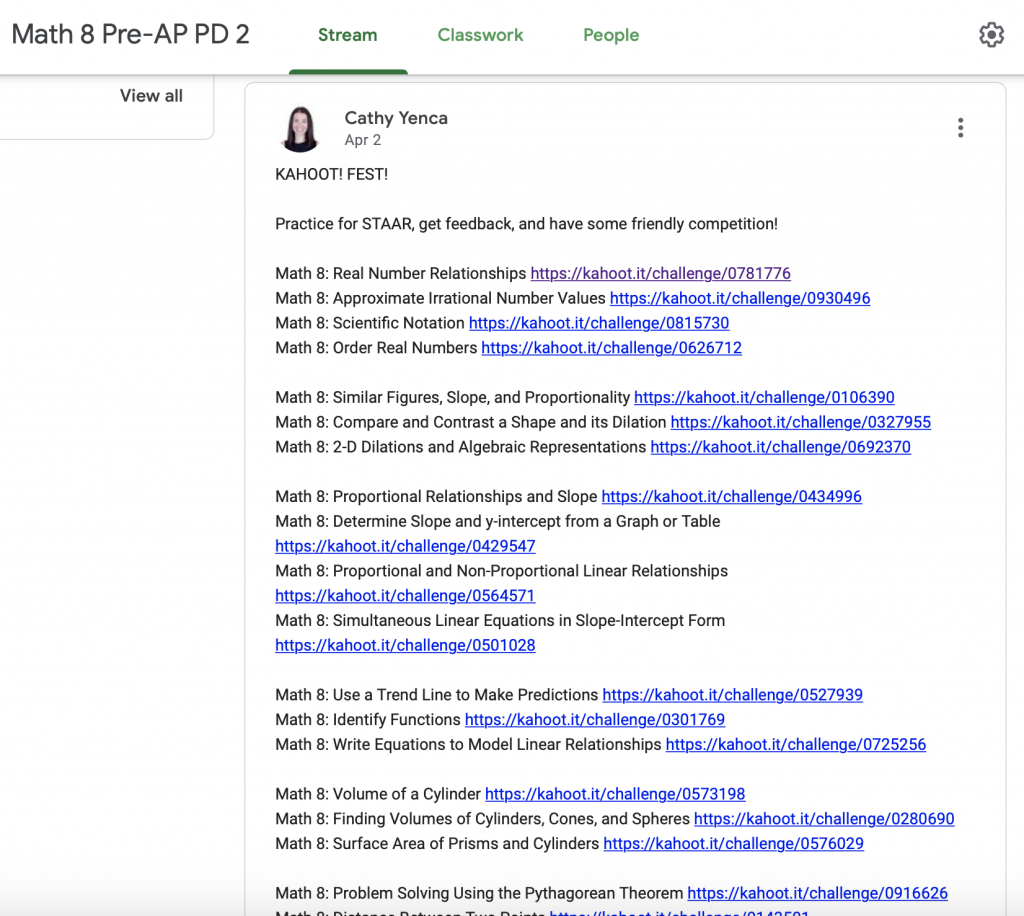
*The resources created and shared by other teachers and me have made the distance feel much closer! I meet with my students “synchronously” for roughly 20-30 minutes during each of our class meetings.
My first goal is to see their faces, chat a bit, and have a light-hearted exchange before getting to the math, the same way we would if we were in “real” class together. I used this Desmos activity during our first Zoom meeting, and here are more! One day, students introduced their pets (lots of folks have shared this idea on the Twitters – thank you!) I got to virtually meet the most ADORABLE hedgehog!!! We are also having theme days. The other day, we wore sunglasses. I have hat day, favorite color day, and even…. bring-a-roll-of-toilet-paper-to-class day coming soon, ha! I also have some fun tasks planned, where having everyone unmuted in Zoom and just calling out when they “see” it will break the ice and start class in a novel way. Here’s one such resource!
I think these will be fun to use during our synchronous Zoom time with kiddos for a light-hearted check-in or wrap-up activity! #SEL #CovidClassroom #iteachmath #iteachmathfromhome #MTBoS #distancelearning @zoom_us Hey @mathequalslove, did you ever make mathy ones? 😉 https://t.co/0rX7G8KSZd
— Cathy Yenca (@mathycathy) April 5, 2020
I’ve also been using our synchronous time to do a “micro teach” and ask students to do a problem or two. When written work is important, I use Nearpod. Having the entire iPad screen to draw and write math work makes Nearpod an ideal tool… and being able to see these work samples, LIVE while using Zoom and Nearpod during our together time, is priceless!
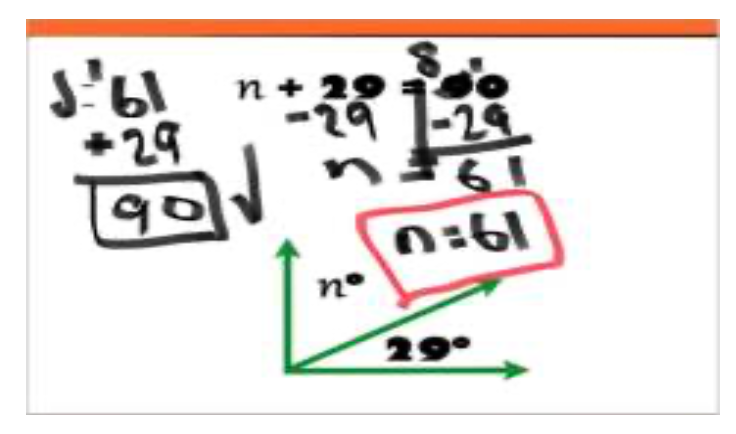
I also like to post a short “quiz” at the end of each Nearpod, because Nearpod allows the teacher to share the quiz results of each individual student through their own, personal pie graph! AMAZING to be able to do this in the classroom when we’re all together… AND now, when we’re all safe in our homes! Here’s one such short-and-sweet Nearpod, where we compared-and-contrasted the simple and compound interest formulas and concepts, worked two problems together during Zoom, students took a very brief to-the-point Nearpod “quiz”, received their pie graph results from me, and were released from Zoom to work on a PDF homework assignment asynchronously for which I immediately posted my key (so they could check work and get feedback before our next class meeting).
I’ve also been using Desmos Activity Builder to create “micro-teach” experiences during our Zoom time. Desmos is great for designing inquiry-based lessons that guide students towards noticing patterns in math and making generalizations.
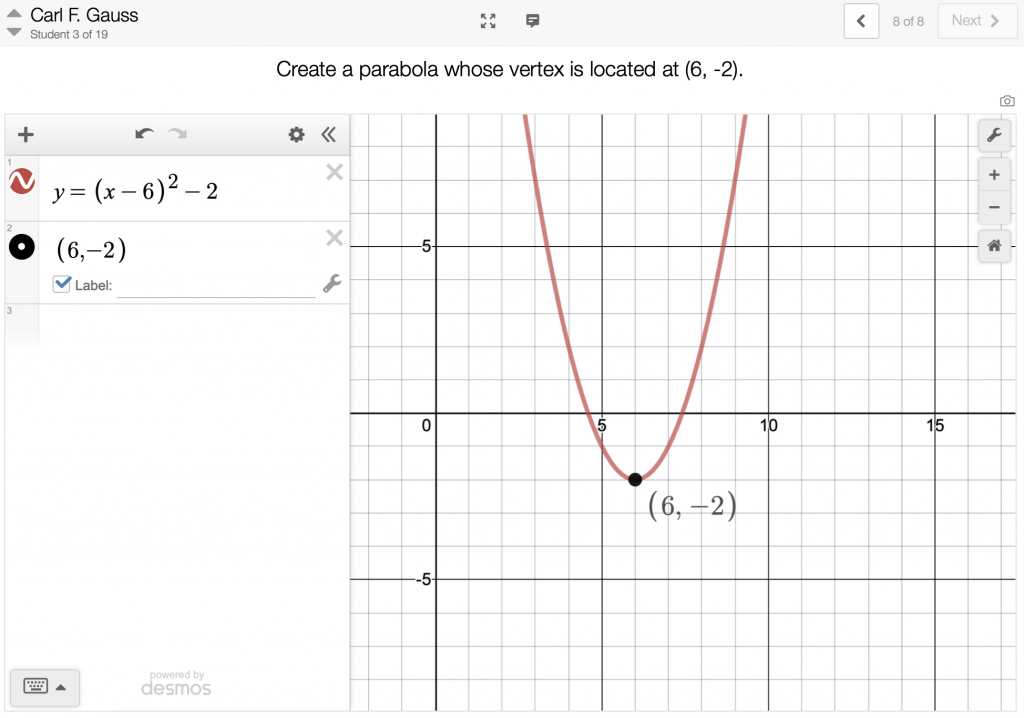
Desmos is also a fantastic place to share short direct-teach videos and ask students follow-up questions that can be seen from the teacher dashboard asynchronously. I’ve been using my OKIOCAM in conjunction with QuickTime or Zoom to create these brief videos for my students. I’ve also had success using a Desmos activity synchronously with the entire class to get started, then using Breakout Groups in Zoom to give students some time to work through more challenging screens together. I can virtually visit their groups while simultaneously watching their work using the Desmos teacher dashboard! Here is a brief lesson I used with my Math 7 crew this past week. Here is a follow-up I will use with Math 8 this coming week. Here is another brief activity I used with Algebra 1, where using Zoom Breakout Groups for the last two screens was ideal!
If seeing S work is priority –> Nearpod (draw feature gives Ss a whole iPad screen’s worth of space to write/draw)
— Cathy Yenca (@mathycathy) April 4, 2020
For inquiry, graphing, thoughtful written responses (including option for each S to see what 3 other Ss wrote) –> Desmos Activities
And… Zoom Breakout groups!
I love the Breakout feature! Used it with a class on Friday during a two-screen Desmos check-in. I “circulated the class” as I would have in person, group to group! Was going to end class so they could work on HW, and they ASKED to be put back in groups rather than leave! 💚💚💚
— Cathy Yenca (@mathycathy) March 30, 2020
I can’t thank the math community enough for continuing to create and share resources and experiences during this time in history!