I learned a nifty domain and range trick from an online workshop about using stickie notes to help “frame” the graph of a function. The idea is to use 4 notes so that all you see is the graph, which can make identifying the domain and range a little easier.
Slide a stickie note from left to right until you “bump into” the function, and stick it on the paper. Likewise, slide a stickie from right to left, top to bottom, and bottom to top, until the graph is framed, like so:
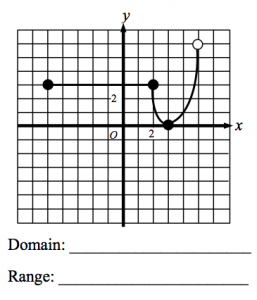
Now, students can see that the domain can be expressed as -5 ≤ x < 5 and the range can be expressed as 0 ≤ y < 6 (It’s easier to see on a graph whose axes are numbered a little better, but you get the idea if you peek at the original graph above).
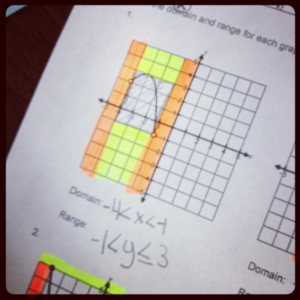
I like the strategy a lot – it’s tough for kids to visualize domain and range with the plethora of unusual and squiggly graphs out there. Since I’m guessing most of my students won’t walk into the EOC with Post-Its in their pockets, I like using highlighters to color-code things a bit. Here are several work samples from students today showing their different interpretations of the strategy. I like how they took the stickie strategy and made it more practical based on the writing tools they *will* have when taking the Algebra 1 EOC next week.
Update!
Check out this idea I found on Pinterest – another nifty way to help students visualize domain and range:

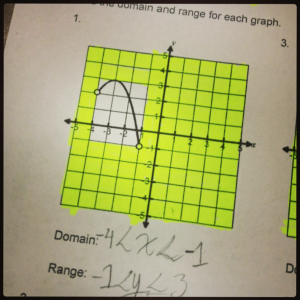
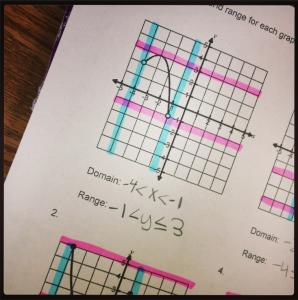















Thank you, thank you, thank you! My Algebra 2 students really struggled with visualizing what domain and range looked like this year. I can’t wait to try this out next year!
Awesome! It was fun to watch my 8th graders pick this strategy right up, and even make it their own! Enjoy!
I think this is an awesome idea and I am trying to figure out how I might possibly be able to apply it to left and right hand limit problems in calculus. Thanks!
I love this idea, but I think kiddos get more confused when they have to deal with infinity and negative infinity. It’s like they don’t understand that the graph does not end when the square grid on your paper ends. Those graphs with arrows on the end they want to stop where they see the graph end. How could you extend this highlighting technique to that concept?
Hi Stacey!
In eye experience, when students “slide” their sticky note or highlighter across an axis to establish when the graph “begins” or “ends”, they’re pretty good about seeing that they can’t draw a highlighter reference or place the sticky because the graph doesn’t have a definitive starting/ending point due to the arrow(s).
To help my students understand about the continuous arrows on a graphed figure:
1) we first review what infinity means and identify the symbol,
2) we then write the symbol on the graph anywhere an arrow appears.