My students celebrated Pi Day on Pi Day Eve. Every year, I give students a Pi Day greeting card summarizing a brief history of pi. When I ask them, “Why is pi slightly larger than 3? Why isn’t it a little bigger than 7? Or 20? Why pi?” the trend continues – I get lots of answers and most of them are completely wrong. It’s worth it to talk about pi, even to students who should already know why pi is pi.
This year, I created “The Ultimate Pi Day” ThingLink, and included both conceptual and novel pi resources. To me, the most powerful resources of “why pi is pi” are the simple Vine video by Nat Banting, and the Approximating Pi Desmos link. Playing the Vine, then the YouTube video about Pi (in 3 minutes and 14 seconds) and ending with the Desmos approximation provided a powerful conceptual combo for students. These links are labeled 3, 1 and 4 below.
 We also had some fun finding our birthdays in pi, listening to pi music, and ending with a memorizing digits of pi contest. I know, I know… this is impractical and some may poo-poo this kind of contest, but let’s loosen up a bit about it all. I don’t think we’re imparting some deep-seated theme that math = memorization here if we balance the activities. Have a little classroom fun, folks. They’re middle school kids, and they eat this stuff up.
We also had some fun finding our birthdays in pi, listening to pi music, and ending with a memorizing digits of pi contest. I know, I know… this is impractical and some may poo-poo this kind of contest, but let’s loosen up a bit about it all. I don’t think we’re imparting some deep-seated theme that math = memorization here if we balance the activities. Have a little classroom fun, folks. They’re middle school kids, and they eat this stuff up.
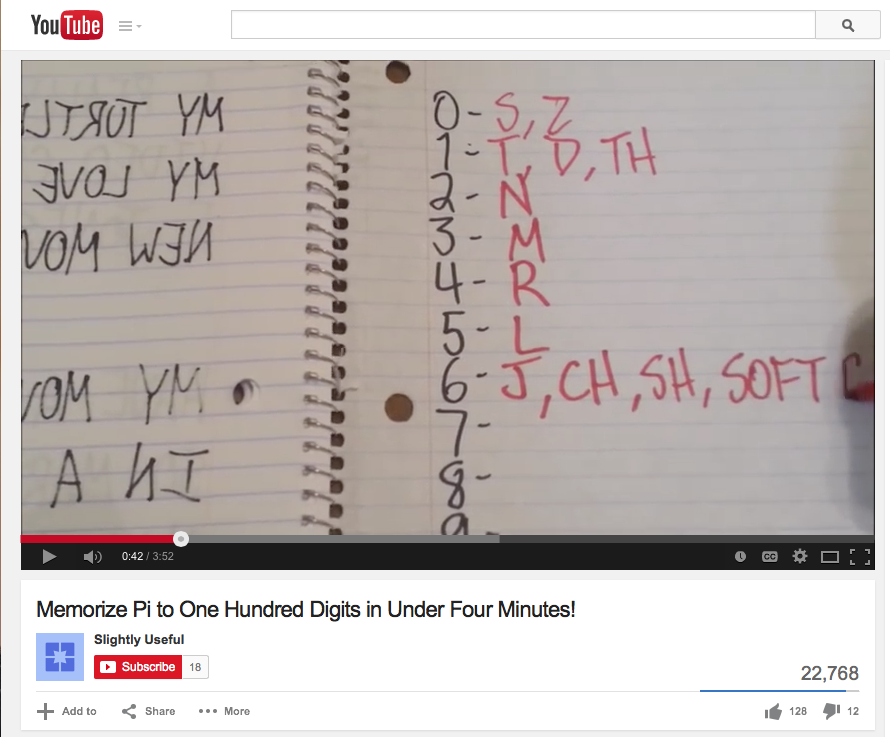
Take Nick. He memorized the first 100 digits of pi, determined to win an autographed Pi print graciously sent to our class by artist Michael Albert. THANK YOU MICHAEL!!! Like many kids these days, he took the task to heart and did the natural thing… he googled “How to Memorize Pi” and found this video on Youtube:
Nick learned the phonetic alphabet and applied this very (complex!) strategy to his pi memorization. He didn’t simply memorize digits – he learned a brand new language, and used it to recite 100 digits of pi. I was absolutely floored. This kid!!!!
 And then there was Skye. She and her mother have been working on the digits of pi all week. When Skye mastered the first 80 digits by mentally breaking them into smaller chunks, mom encouraged her to keep going. Together, they also worked on the first 100 digits. To be sure to take the win, Skye learned 103 digits and walked away, proudly, with Michael’s pi print. For the record, Michael sent an entire collection of his autographed prints to us, so the top pi memorizer in each of my classes received a different piece of art.
And then there was Skye. She and her mother have been working on the digits of pi all week. When Skye mastered the first 80 digits by mentally breaking them into smaller chunks, mom encouraged her to keep going. Together, they also worked on the first 100 digits. To be sure to take the win, Skye learned 103 digits and walked away, proudly, with Michael’s pi print. For the record, Michael sent an entire collection of his autographed prints to us, so the top pi memorizer in each of my classes received a different piece of art.
His generosity was the icing on a Pi Day (Eve) we won’t soon forget.
A Very Happy Pi Day to you!



















I love how you use Thing Link with your students! My middle school students are not allowed to have the app because the rating is too high. Did you have that problem at all?
Hi Kimberly – Did you know earlier this week, ThingLink announced that their mobile app is now rated 9+? I hope that helps you! See my previous post about the changes ThingLink has recently implemented to make it more classroom-friendly! 🙂
Hi Cathy,
Here’s an easier strategy to learn numerous digits of pi. http://memorizingpi.blogspot.com/
It’s a mnemonic system that’s much easier to learn compared to the one in the video, because translating the letters back to numbers is simple. Your students can even write their own stories to memorize pi or any other strings of numbers.
Thanks for the tip! I left the strategies entirely up to my students, and found the variety in their methods so interesting!
Have you seen pi as a generalized Continued Fraction???!!! It is, lie the square root of 2 and phi, so much easier to understand!! Please teach your students about Continued Fractions and open their eyes to the wonderful patterns hidden in numbers!!
Also, there is the Theory of Neutral Operators, whereby two (or more) operators are held neutral to each other between constants. So, for example, if we let a+b = a*b = c, then subtract b from both sides and factor the right side, we have a += b(a-1). Then, by SIMPLE ALGEBRA, if we divide both sides by the term (a-1), we have a/(a-1) = b, and because both Addition and multiplication are commutative, b/(b-1) = a as well (we could have started by subtracting a). We have now isolated and defined b (or a) in terms of a and 1 (or b and 1). Given a then, we may determine b, except that a may not equal 1, lest we have division by 0 in the denominator (though allowed for the tangent y/x slope of 90 degrees being Infinity in the Cartesisian Plane, so that INF * 0 = -1, and the axes are perpendicular). Whatev. Let’s say that a=5, then 5/(5-1) = 5/4 = b and. testing our original hypothesis, we find that 5+5/4 does equal 5* 5/4 = c = 25/4. This works for F = m*a = m+a, E = mc^2 = m-c^2, a^2 + b^2 + c^2 = either a^2 / b^2 or a^2 * b^2. It alters every formula ever. It’s a “Tipping Point” in Nature between Length and Area for one thing … perhaps .. given addition is length and multiplying creates area. Solving ab = a^b goes like this: ab/a = (a^b)/a; b=a^(b-1); b^(1/(b-1)) = a, which is now isolated and defined. Solving a-b = a/b goes like this: a-a-b = a/b -a; -b = a(1/b – 1); -b/(1/b – 1) = a; b/(1 – 1/b) = a, which is isolated and defined. I have about 425,000 views on wikiHow.com under the ids xhohx and Christopher G. on how to turn trig into art, algebra, more Neutral Ops (my theory), some Euclid and some business & finance … 134 articles written over about 2 years so that if each article view is a person’s 4th visit, then that’s 50,000 students/year approximately. Hooray for you for getting on the net where a real impact on the math deficit may be made!! Hope I’ve helped!! Please visit wikiHow.com — lots and lots of teens and other youngsters do. They’re very bright!! 😀
https://plus.maths.org/content/chaos-numberland-secret-life-continued-fractions
Commutation = Symmetry, which is very hot in higher math right now …
http://www.wikihow.com/Start-Working-with-Continued-Fractions
Phi = (sqrt(5)+1)/2 = 1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+1/(1+…)))))))))))
In Continued Fraction notation:
e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, …]
sqrt(2) = [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, …]
sqrt(3) = [1; 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, …]
π = [3; 7, 15, 1 292, 1, 1, 1, 2, 1, 3, 1, 14, 2. 1, 1, 2, 2, 2, 2, 1, 84, 2, …]
If you read my article, you will see other representations of π that are just as amazing!
Thank you so much! This is exactly what I was looking for!
Woot!