I first experienced some form of this activity with the amazing Dennis Ebersole in a workshop years ago. When we played the game, if memory serves me, the goal was to provide a motivating way for students to practice integer addition. (Or was it? One thing I learned from Dennis, through his constant modeling, was that the tasks he provided to teachers had layers that were up to US to discover. When anyone asked him any sort of question, he giggled, shrugged his shoulders, and sometimes said, “I don’t know..?!?”)
Back to the game. Here’s how we play.
The game board is simply a grid with integers and an “x” to mark the starting position. Choose the integers you like. Next, we need two teams. A spokesperson who can handle the pressure of making a team decision in spite of potential disagreements is essential to classroom sanity. 🙂 One team can only make horizontal moves, and the other team, vertical moves.
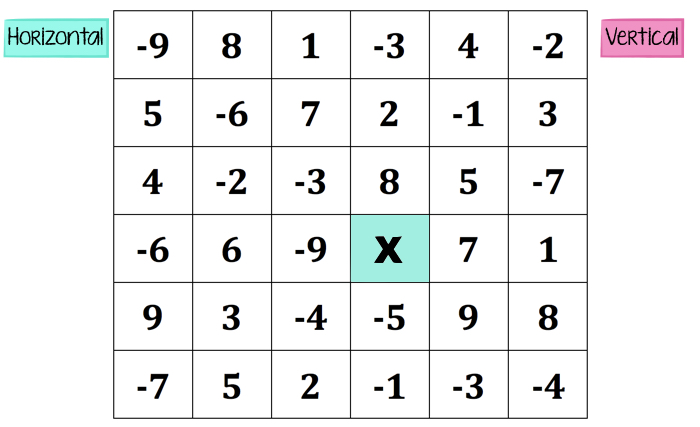
Let’s say horizontal movers arbitrarily go first. Starting at the “x”, the team gets to decide which number in that row only they’d like to have. That number represents the points earned by their team. (Note: Sometimes students realize in this moment that we need to establish how a team wins this game. Most points? Least points? Closest to zero at the end? They come up with a lot of creative ways to win.)
For this example, let’s say the teams establish that the MOST points at the end wins the game. So, team horizontal chooses the 7, and earns 7 points. Now, that 7 is used up. Done. Circle it and keep a running total of points earned.
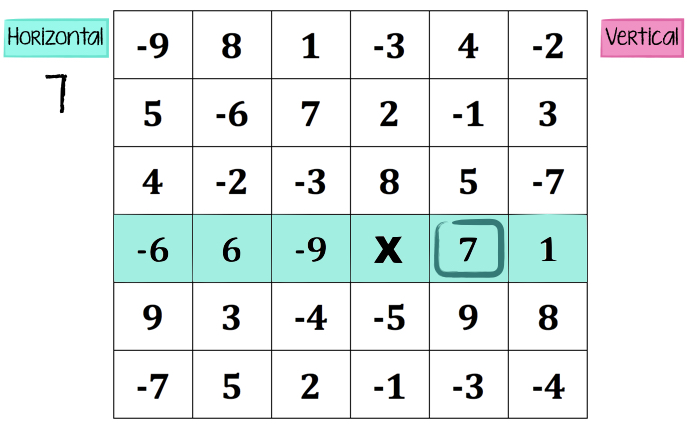
Now it’s team vertical’s move. Since the other team chose the 7, team vertical must choose an available number in that column only, and they’ll receive that number of points.
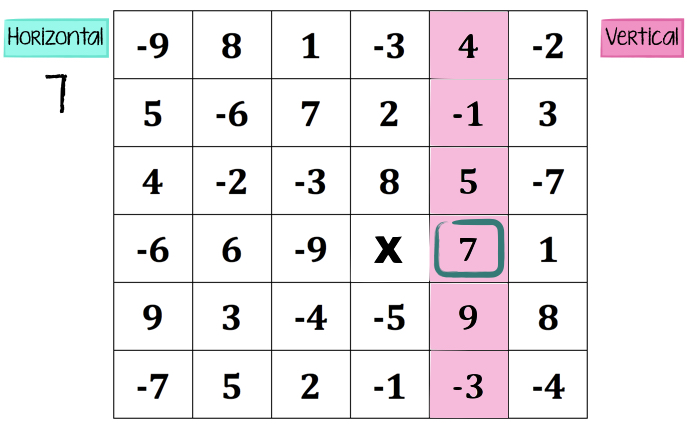
Being new to this game, that 9 is probably pretty tempting. So, team vertical chooses the 9 and earns 9 points. Back to team horizontal we go… and either BEFORE team vertical chooses that 9, or just AFTER they do… everyone is realizing that there’s a bit more strategy to this thing than they realized at first glance. (Remember when I said each team needs a spokesperson for classroom sanity? That’s to preserve YOUR sanity, teacher! 🙂 That spokesperson has to make each choice based on team feedback, so you know who to listen to for the final decision on each move. Let’s just say this gets passionate. FAST.)
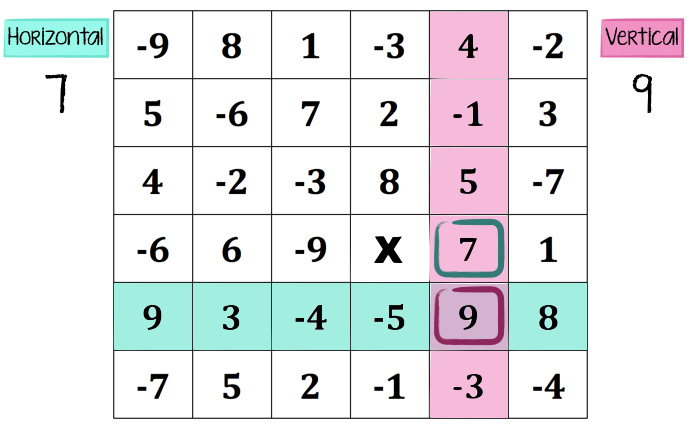
Eventually, either every number is used up, or a dead-end occurs and the game ends. I like to play at least ONCE as a whole-class activity with a spokesperson for each team, and then have students play in pairs.
Fun Things That Often Happen
Sometimes, it doesn’t occur to either team to establish how we win. This can get very interesting when it comes to strategy. One team starts aiming for the biggest numbers, and the other team aims for the smallest numbers… with every turn, students confuse their opposing teammates with their point choices, and mid-game, someone finally says, “Why are you choosing those numbers? Wait, does the SMALLEST score win?”
“Does it?” say I (and Dennis would be SO proud of that response).
It’s also really cool when teams make up unusual rules for how to win. The other day we played, and several students had an idea. They thought we should find the mean of the two final team scores at the end. Then, look at how close each final team score was to this mean value. The team whose score is closest to the mean score, wins…
… and so we follow this victory rule… and the teams TIE! Not with a nice value, but each team is exactly the same convoluted decimal distance from the mean! It’s a miracle! How did this happen?!? The class goes BONKERS and wants to play again, under these same circumstances.
And I am biting my tongue and practicing my best poker-face.
We play again, and AGAIN, a perfect tie! This time, the distance each team’s score is from the mean is less obscure, but it’s the SAME! Again! Are we amazing, or what?
Wait for it…
“… wait, Mrs. Yenca. Will this happen EVERY time?!?”
What do *YOU* think?
How do you know?
School’s out for summer for me… but is it for YOU? Give this integer game a try, and share any new strategies you or your students come up with!

















Pingback: July 2018: What's News in Education - Maths Pathway
Pingback: July 2018: What's News in Education | Maths Pathway