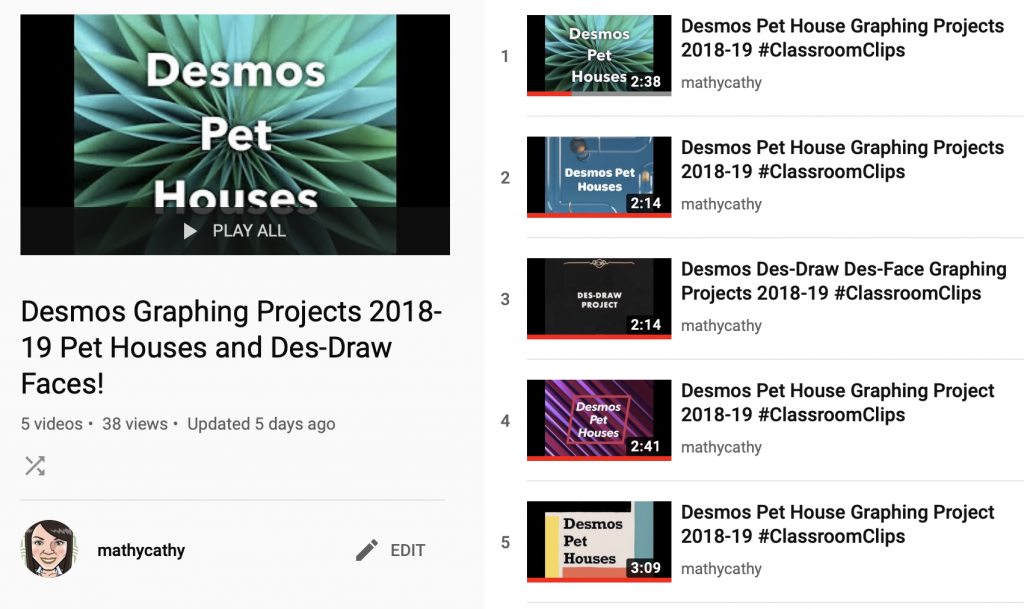
Here in Texas, we received official word from our governor that our classrooms are closed for the remainder of the school year. We knew this was coming. It still stings. Such an abrupt ending to the communities we’ve built since August. I can’t believe our before-spring-break farewells were actually the last time we’d meet in room 510… heartbreaking!!!
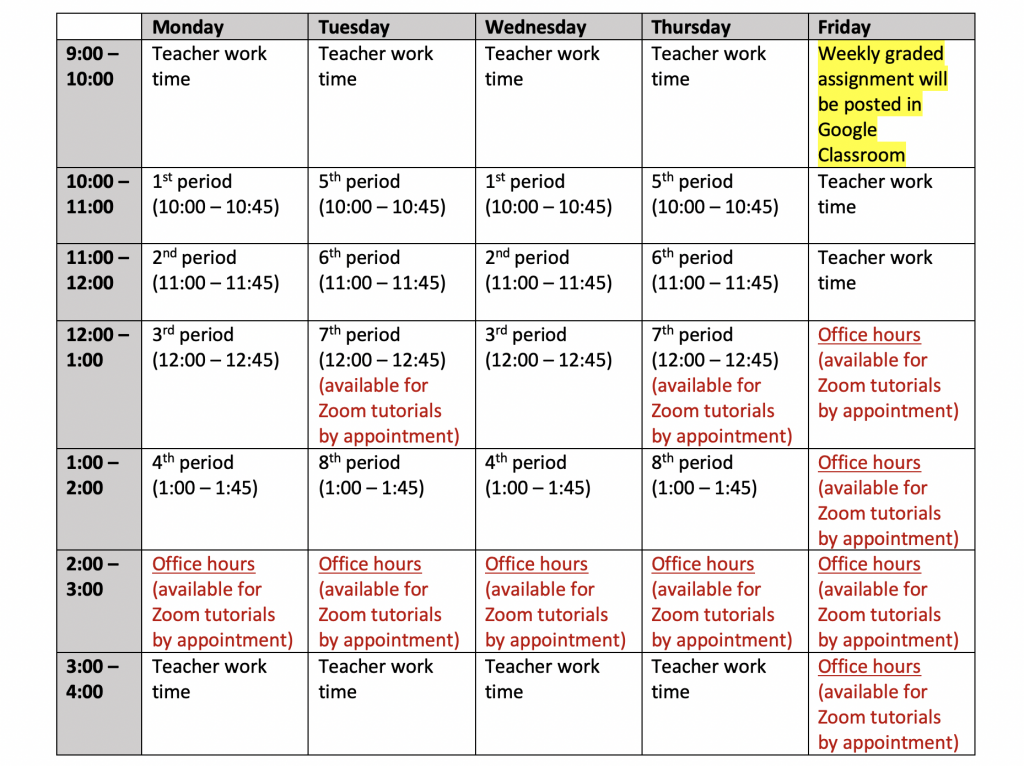
Meeting twice weekly on Zoom from home sure helps! We’re keeping our communities and curriculum rolling in the best ways we know how. It has been exciting and exhausting to transition to 100% online learning. I lost a LOT of sleep the first few days, and worked well into the night hours trying to adjust materials I had, or create things from scratch, to make them more distance-friendly. Even when we regularly use technology tools in our classrooms, it’s with the assumption that our students are ALSO right in front of us! That we can run around the classroom and LOOK at what they’re doing, and CHAT with them one-on-one, in small groups, and as a whole crew. Online learning has been a blessing and a challenge.
Looking ahead to the rest of this Maypril of a school year, I have some Desmos projects and enrichment activities up my sleeve. Since I teach three math courses, I thought I’d share the resources I’ll likely use for each class here in this post.
{Math 7}
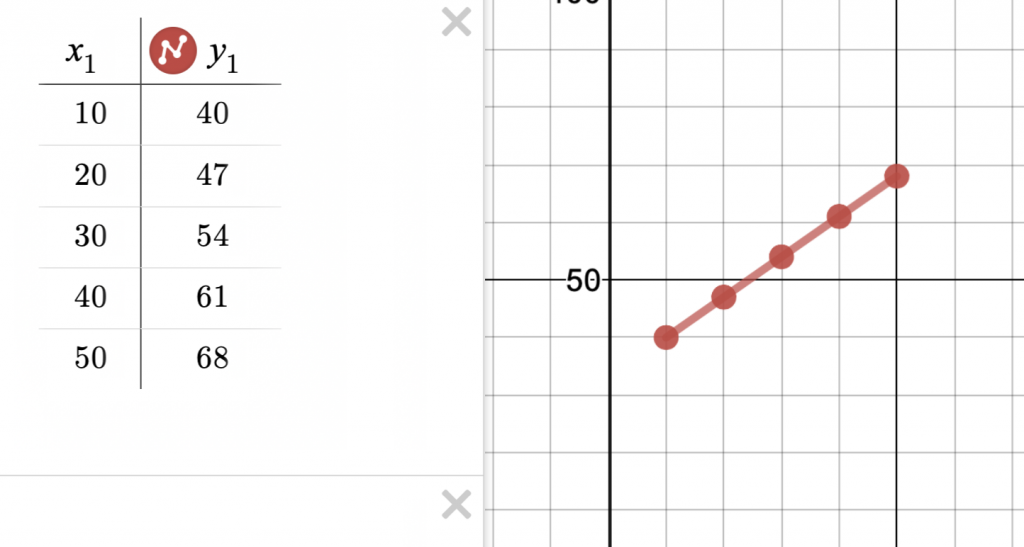
Math 7 students will use tables of connected points in this Desmos FIRST NAME Art Project. The included checklist could be modified to include point values if one chooses to ‘grade’ the project. Thanks to the ability to copy-and-paste screens from one Desmos Activity to another, this mash-up includes modified screens from other activities (credit given in the project description). Students are also asked to capture and submit a photo of a graph paper ‘rough draft’, thanks to the ability to add an image to a Desmos graph!
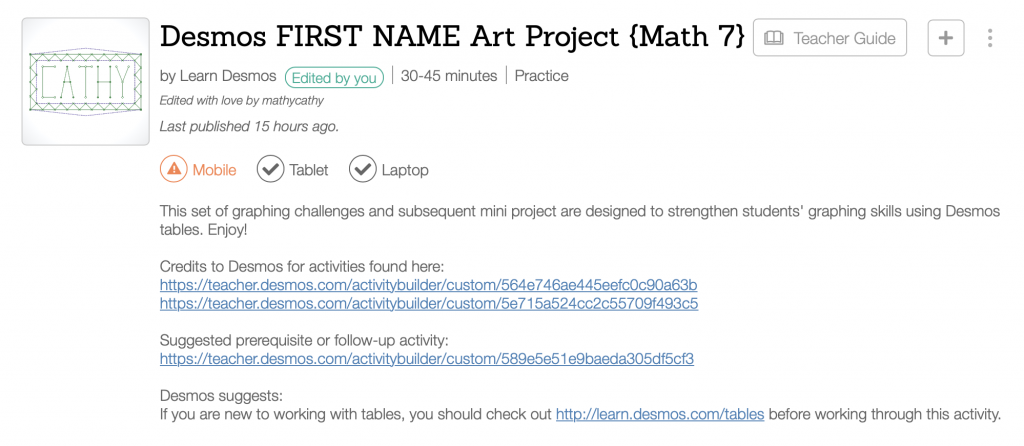
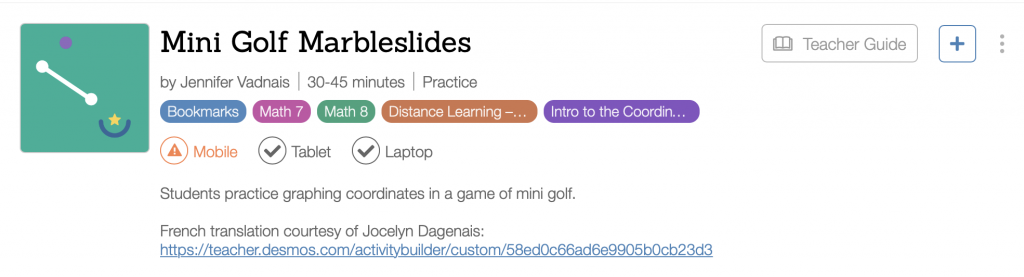
Looking for a prerequisite or follow-up activity that helps students use Desmos tables for graphing… and fun? Try Mini Golf Marbleslides!
To revisit ratios and proportional reasoning one last time, while previewing the concept of scale factor (which will be addressed in Math 8 next year) students and families will choose a favorite recipe, then use this Desmos project to scale it up as if they were feeding our entire class… and me!
My PLC-mate Lauren and I have been throwing around the idea of a recipe project, and thanks to the Desmos Educators group on Facebook, and friends on Twitter, we got the help we needed to include some self-checking CL tables. Once students scale up the recipe, they’ll add their recipe AND scaled-up recipe to a Google Slides presentation, which will serve as a virtual class cook book to end the year!
{Math 8}
This will be the third year my Math 8 students will use linear functions, and a whole lot more, to create their Pet House Linear Projects! This year, I added a screen where students capture and submit a photo of a graph paper ‘rough draft’ since we won’t be in the classroom together. If you search for this project online, you may also find modifications folks have made that include other features and some fancy CL (computation layer)!
As a prerequisite to Pet Houses, perhaps Marbleslides: Lines will help students get reacquainted with linear functions?
To encourage students to explore functions beyond linear, here are two enrichment tasks that can ‘run in the background’ as students build their Pet Houses. I also use these for my Algebra 1 students! MARBLESLIDES CHALLENGE SETS!


{Algebra 1}
While the Pet House Project focuses mostly on linear (but never stays there, ha!) this Des-Draw Algebra 1 project explicitly asks for quadratics to be included… and nudges students to explore inequalities as well as functions beyond linear and quadratic.
As a prerequisite to Des-Draw, maybe Marbleslides: Parabolas will help students get reacquainted with quadratic functions?
Lastly, these BREAKOUT activities might be even MORE challenging in a distance-learning environment, but I have them in my virtual back pocket nonetheless. Differing opinions were shared about trying to combine the Zoom Breakout feature with a Desmos Breakout activity… you never know until you try…?! What do YOU think?
Has anyone used @zoom_us breakout rooms in conjunction with a @Desmos breakout?`
— Cathy Yenca (@mathycathy) April 10, 2020
If so, how’d it go?
Plan: Each S would have to ‘break out’ on their own iPad at home, while working together with their Zoom group.https://t.co/b9xOEBwqRh#iteachmath #MTBoS #iteachmathfromhome
What? You’ve never heard of Jay Chow’s DESMOS BREAKOUT ACTIVITIES?!?! Launch one for yourself, try to ‘break out’ as a student, and you’ll quickly see why these activities have become a few of my favorite ways to promote practice, review, and deeper understanding of concepts.
Breakout Desmos – LINEAR!
Breakout Desmos – QUADRATIC!
These activities are literally the tip of the iceberg as far as what’s available. Googling “teacher Desmos *insert math topic*” will provide even MORE options for you! I hope your end-of-year Desmos-From-a-Distance experiences are successful for you and your students! Thank you to ALL who have contributed to the creation of so many rich (and fun) Desmos activities!