 Texas Math 8 standards provide students with a firm foundation of linear concepts and slope-intercept form. Additionally, my Math 8 kiddos just wrapped up a polynomials enrichment unit. With this in mind, I felt like they had a solid background to ensure success with generalizing patterns algebraically. What better way to do this than with “Visual Patterns”!
Texas Math 8 standards provide students with a firm foundation of linear concepts and slope-intercept form. Additionally, my Math 8 kiddos just wrapped up a polynomials enrichment unit. With this in mind, I felt like they had a solid background to ensure success with generalizing patterns algebraically. What better way to do this than with “Visual Patterns”!
I’m pretty new to using “Visual Patterns” with students, and in the past, I didn’t feel like I introduced these very well. Students could draw and describe the pattern, but when it was time to complete a table beyond the first few figures, they had a tough time expressing themselves algebraically. I think the most popular equation was… y = IDK.
Before I began a few days with “Visual Patterns” this week, I sought expert advice from the #MTBoS and found this video of Jo Boaler sharing various student strategies to be quite helpful in shaping my questioning. Additionally, Jo’s animations and unconventional (fun) pattern descriptions made me realize that I wanted to truly capture student thinking, ALL students’ thinking, possibly in words AND through visuals. Could I also provide students with an animated view of pattern growth the way Jo did? (Note: Keynote “Magic Move” and a #SilentSolutions video helped make that happen!)
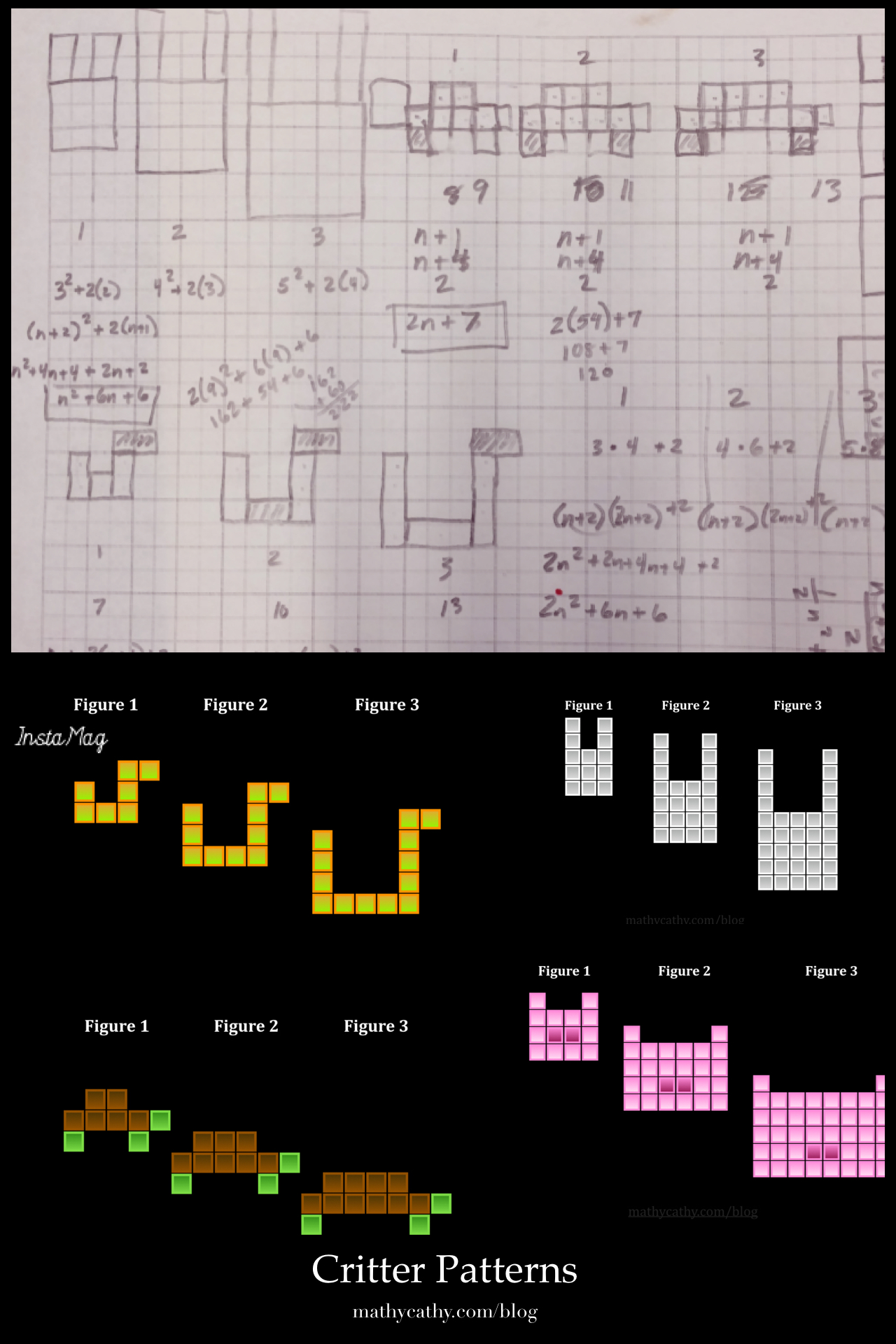 First, my son and I sat on our patio with graph paper, designing our own “Critter Patterns” to represent some of our favorite animals. I translated our sketches to Keynote slides that represented Figure 1, Figure 2, and Figure 3 of each pattern. I purposely created two patterns that were linear, and two that were not.
First, my son and I sat on our patio with graph paper, designing our own “Critter Patterns” to represent some of our favorite animals. I translated our sketches to Keynote slides that represented Figure 1, Figure 2, and Figure 3 of each pattern. I purposely created two patterns that were linear, and two that were not.
Next question – pattern delivery to students… Desmos Activity Builder? Or Nearpod?
I couldn’t choose, so I tried both, in my own little experiment.
I made this Desmos Activity Builder and used it to introduce Critter Patterns to the first of my three Math 8 classes. I used this Nearpod to introduce the patterns to the second class.
For my third class, I decided I would use either Desmos or Nearpod, depending on which delivery format seemed to go better.
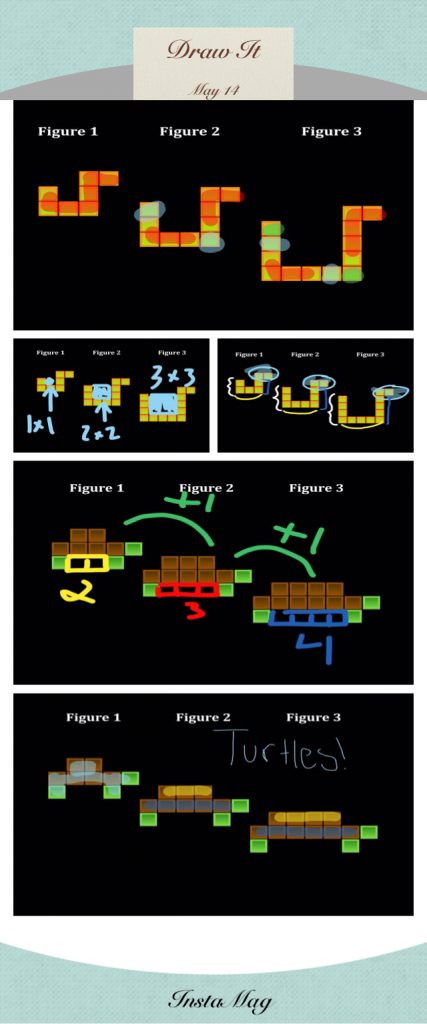 There was incredible value in giving students the chance to examine the pattern closely, and “Draw” the way they saw it growing using Nearpod. Asking students to describe the pattern in words right off the bat in the Desmos lesson version proved to be more challenging. I heard a few grumbles of what-are-we-even-doing-right-now, which told me that the “Draw” had a bit of a lower floor for these Visual Patterns newbies. Since any URL can be added to a Nearpod lesson, I was able to integrate a prepared Desmos calculator slide at just the right time in the Nearpod lesson (this Desmos-Shows-Up-In-A-Nearpod gig amazes students every. single. time.)
There was incredible value in giving students the chance to examine the pattern closely, and “Draw” the way they saw it growing using Nearpod. Asking students to describe the pattern in words right off the bat in the Desmos lesson version proved to be more challenging. I heard a few grumbles of what-are-we-even-doing-right-now, which told me that the “Draw” had a bit of a lower floor for these Visual Patterns newbies. Since any URL can be added to a Nearpod lesson, I was able to integrate a prepared Desmos calculator slide at just the right time in the Nearpod lesson (this Desmos-Shows-Up-In-A-Nearpod gig amazes students every. single. time.)
Overall, the Nearpod lesson slowed students down to examine and draw the patterns out, and sharing student drawings at the front of the class was effective and immediately enjoyable. So many different ways to see the same thing! That’s not to say that Desmos wasn’t effective – it was just a bit of a bumpier start. You’d never know it, looking at the activity’s history in my teacher dashboard – having the ability to self-navigate and revise in Desmos Activity Builder clearly had its perks too.
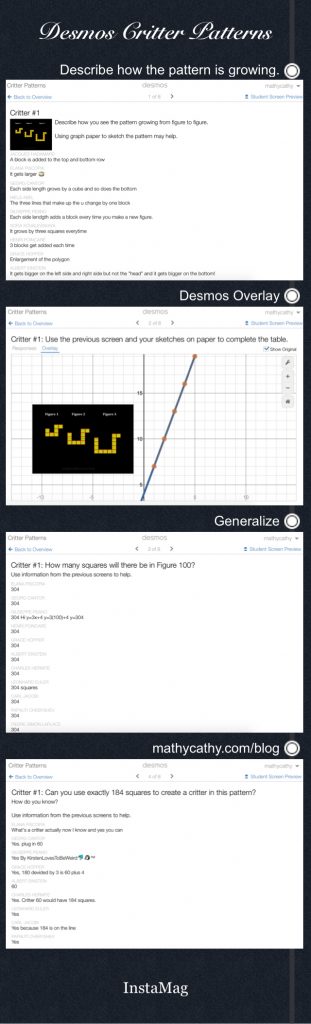 After my Desmos/Nearpod experiment to introduce patterns, I opted to use Nearpod to introduce the rest. I used Fawn Nguyen’s Visual Patterns as homework each day. To begin each class following our introduction lesson day, I used blank Nearpod Draw slides to gather student thinking for whole-class discussions of the homework patterns. Note: Linear patterns went VERY well, and nonlinear patterns varied from students absolutely NAILING IT to the infamous y = IDK. These students lack experience with quadratics, and some of them sought help from older siblings and parents. I loved how families got involved in generalizing more challenging patterns! I was *hoping* students would see some of these in ways that I hadn’t. I can’t unsee my own way.
After my Desmos/Nearpod experiment to introduce patterns, I opted to use Nearpod to introduce the rest. I used Fawn Nguyen’s Visual Patterns as homework each day. To begin each class following our introduction lesson day, I used blank Nearpod Draw slides to gather student thinking for whole-class discussions of the homework patterns. Note: Linear patterns went VERY well, and nonlinear patterns varied from students absolutely NAILING IT to the infamous y = IDK. These students lack experience with quadratics, and some of them sought help from older siblings and parents. I loved how families got involved in generalizing more challenging patterns! I was *hoping* students would see some of these in ways that I hadn’t. I can’t unsee my own way.
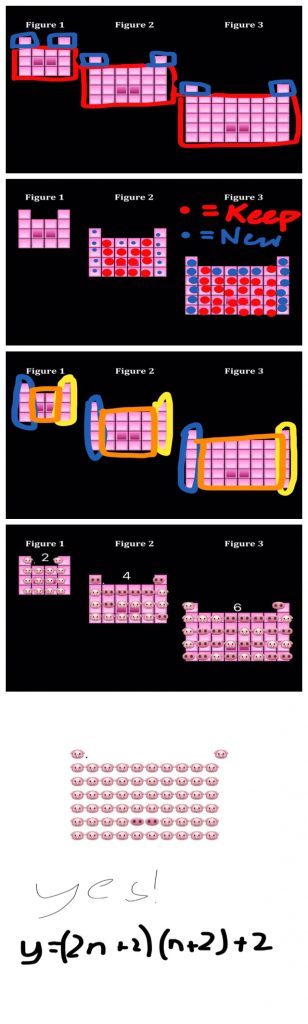
Reluctantly, I showed “my way” for each of the quadratic patterns. They followed along as I got them started, paused short of spilling ALL the beans so that they could take my strategy to the finish line, and as a result, many “got it” when it was time to generalize. How do you handle it when kids can’t generalize? Do you show them the way, or just leave it for them to potentially play with? I dunno. “You can always add. You can’t subtract.” What’s been seen has been seen, this time.
Highlight: Students taking on my here’s-how-I-started-now-run-with-it, ending up with a table, function, and graph in Desmos, and seeing them cheer when a parabola appeared, passing through all of their points. They don’t even know what a parabola is, but they DO know it’s a good thing when a nonlinear graph passes through their table’s points. Super fun to watch this!
After several days of this cycle, and exploring both linear and nonlinear patterns, I saw students’ confidence grow mathematically. Through various Nearpod “Draw” experiences, I saw student creativity as well!
Next up – I’m asking students to create their own “Visual Patterns”. Student groups will each create one linear and one nonlinear pattern, as well as other components, and showcase their work in a Book Creator eBook. Stay tuned to see our student-created Visual Patterns mini-eBooks!
For your viewing pleasure, here are more student work samples from this week.
My Nearpod “Reports” are a treasure-trove of student thinking.


















Pingback: Student-Created Visual Patterns and Book Creator | MathyCathy's Blog – Mrs. Cathy Yenca
Thanks so much for sharing! These Visual Patterns my favorite to teach!! I’ve been trying to figure out how to do it virtually!
When I click on the “this Nearpod” link, it tells me the code is invalid. Could you please share your Nearpod lesson with me? I’d REALLY appreciate it!
Try These! 🙂
https://share.nearpod.com/e/HoE9gDTrQab
https://share.nearpod.com/e/FvYxXwVrQab
https://share.nearpod.com/e/ZeHUBuWrQab
https://share.nearpod.com/e/cVRnbnXrQab