My Algebra students completed a cooperative quadratic QR-code walk-about type task the other day. They could work with a partner, use a graphing calculator, Desmos, the HMH Fuse app, their homework, notes… everything. They scanned various QR-codes, which revealed practice problems for them to each complete on a paper work template. The idea was to facilitate an environment where conversation was rich and necessary. I find that my face hurts at the end of classes like this because I’m just so darn tickled to hear my students talking, justifying, and using academic vocabulary appropriately. It’s fun to literally watch them learning… and even MORE fun to watch them TEACHING.
Amidst all this bliss, something quite bizarre happened that caught me completely off guard. Problem A Part 2 seemed direct and unassuming to me… yet every. single. solitary. student. got. it. wrong.

Students shared with me that they “didn’t know” they could rearrange the ordered pairs… or that I “never told them” they could do that.
I’m like… WHAT?
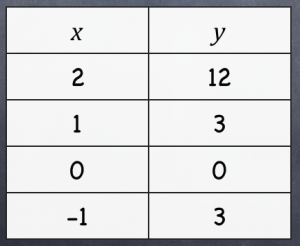
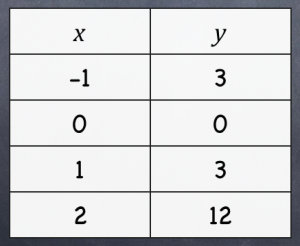
This misconception was common between all three of my algebra classes. They looked at the x-values, and decided this couldn’t possibly be quadratic… if the x-values appeared to have no consistent differences, why even bother looking at the y-values…?!?
Needless to say, I did a little reteaching and represented the ordered pairs in tables like these, but this was not a misconception I had anticipated.
How do you handle it when students think weird, unanticipated stuff? When they create rules that aren’t there, and abide by them… en masse?
















I’m sure many of the readers run into situations like this one as well! I think the part where you said “…when they create rules that aren’t there, and abide by them…” is key. I think students are so programmed to think of math as rules that they don’t really picture what the problem really looks like.
I believe the culture of “find the answer and move on” that we promote in math education doesn’t promote problem solving at all. Even in problem solving questions we give students rules/frameworks/acronyms/etc. to help them think less about what is really happening and more about how to do the problem with as little thinking as possible.
Seems like we are converging on a similar topic as a recent post discusses here about rules, steps, tricks and formulae in math class.
Thanks for sharing your post with us!
Thanks for stopping by, Kyle! Through our conversation, I thought about this resource too – check it out: http://nixthetricks.com An aside – I’ve tried commenting on your blog, and it never lets me through 🙁 Your blog thinks I’m spam, HA!
This QR quadratic activity sounds cool! Do you have it available anywhere?
Here’s a similar activity: https://www.teacherspayteachers.com/Product/Factoring-Monomials-Polynomials-Practice-with-QR-Codes-FREE-524295