About a year ago, Nathan Kraft blogged about a collaborative lesson design and experience to help students understand (and WANT to understand) the concept of mean absolute deviation. This standard was added to 8th grade curriculum here in Texas three years ago, and the past two years, I feel like my MAD lessons could have been better. Nathan’s post was exactly the boost I was looking for. Thanks to Nathan’s detailed lesson notes and student work samples, I designed this Desmos experience, and started class with it today.
Students went from ‘Monday groggy’ to actively engaged in about three seconds. First, I used Desmos’ new “teacher-paced gates” feature to limit students to only the first three screens. The teacher simply clicks on the first and last screens he/she wants students to be able to access.
In pairs, I let them roll for a few minutes and pressed “pause” to bring everyone together. So glad I did this – we were able to scroll through graph screens to see who “won” at their first stab at “The Sum Game” (that is to say, which partner got closer to a sum of 7). P.S. Using a pair of virtual dice on Random.org and the split-screen feature on our iPad Air 2s was nifty!
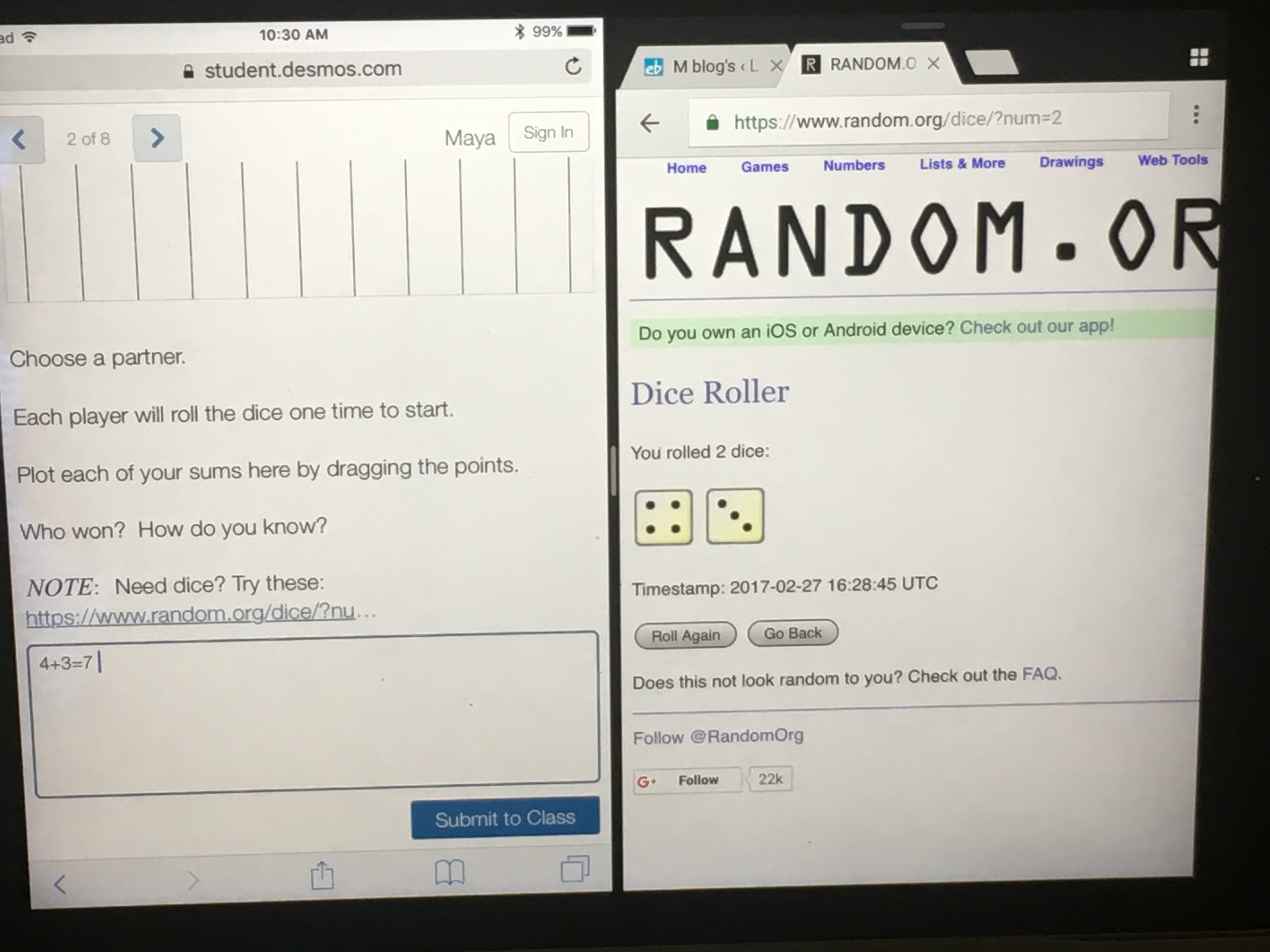
Split Screen!
The seed was planted that a sum of 5 ties with a sum of 9, and we were off with our second “teacher-paced gate”. This time, student pairs only had access to screens 4, 5 and 6, where each partner “rolled” the pair of virtual dice to find two sums. So many interesting things happened here when partners decided on the victor. For example, if one student rolled a 7, many students completely ignored the other rolls, establishing the 7-roller as the winner, period. Some students started finding the sums of both rolls together to try to establish who won. Some students computed averages, but averaged the two sums without regard to the distance from 7. Again, I paused (They HATE when I pause without warning them! They HATE when I pause WITH a warning! They HATE BEING PAUSED… but it’s SO NECESSARY and helpful for class discussions! Students be like, “AWWWWW!!!!”) and we addressed who won in each case. Check out some interesting explanations below that provided opportunities for class discussion. 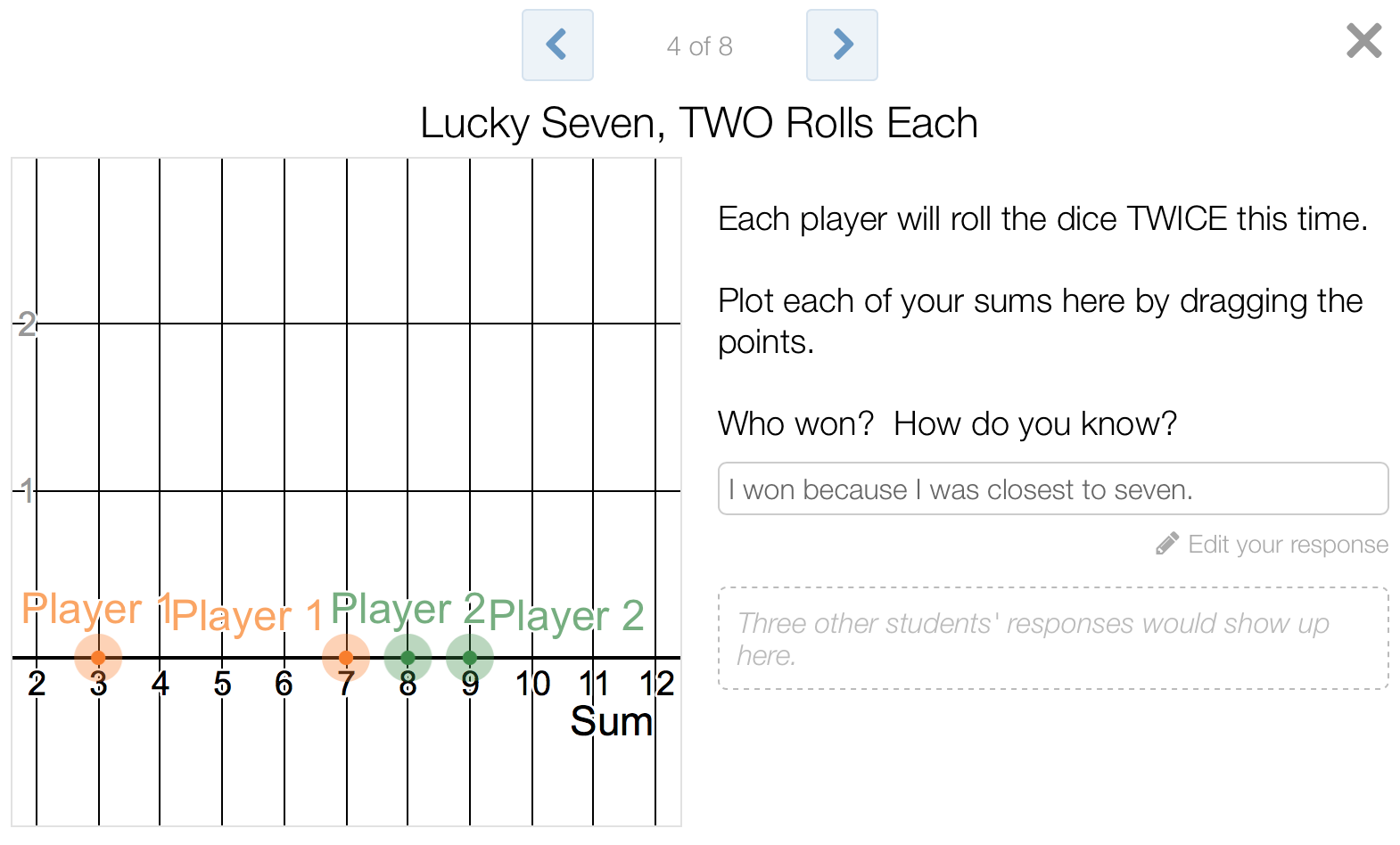
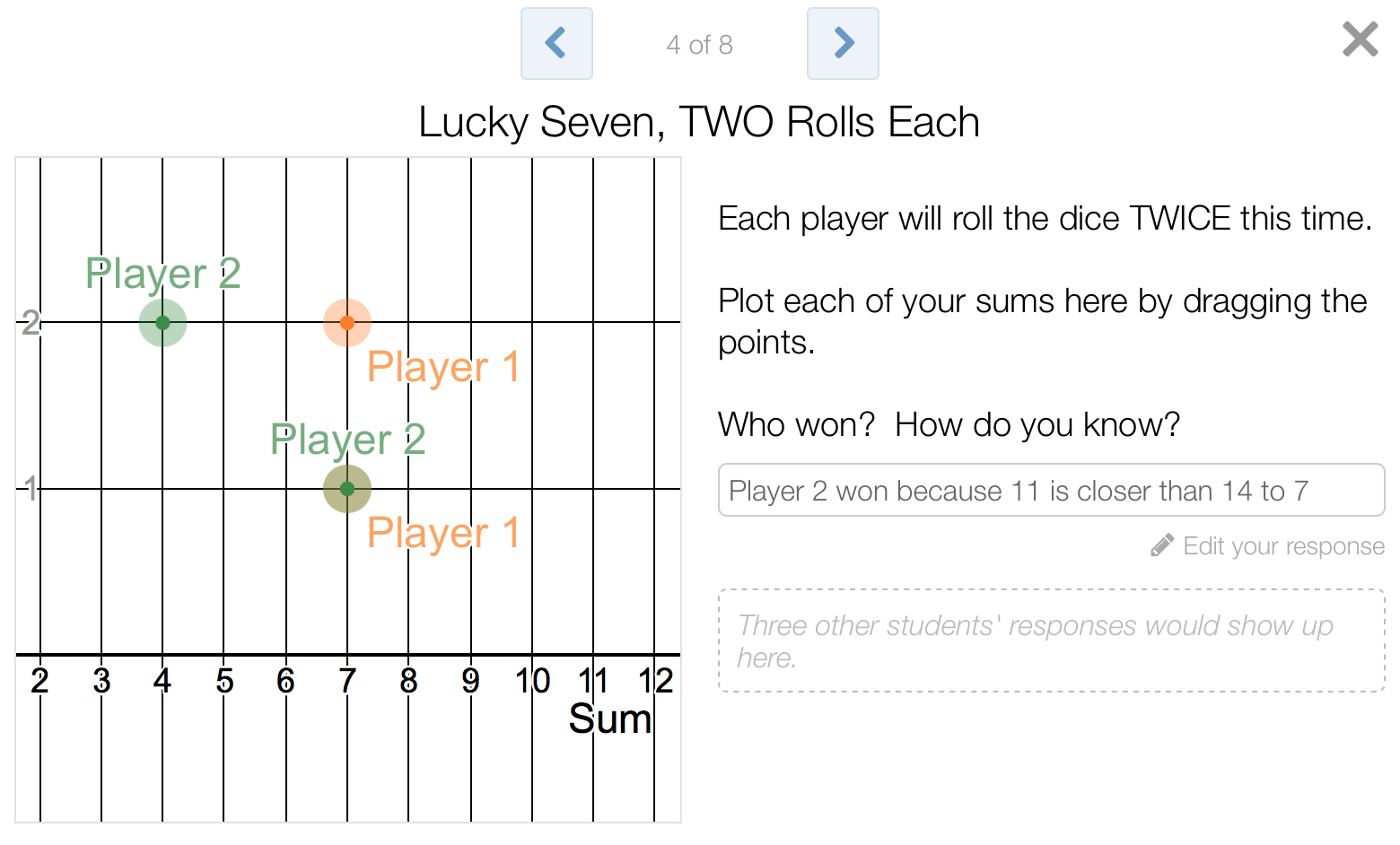
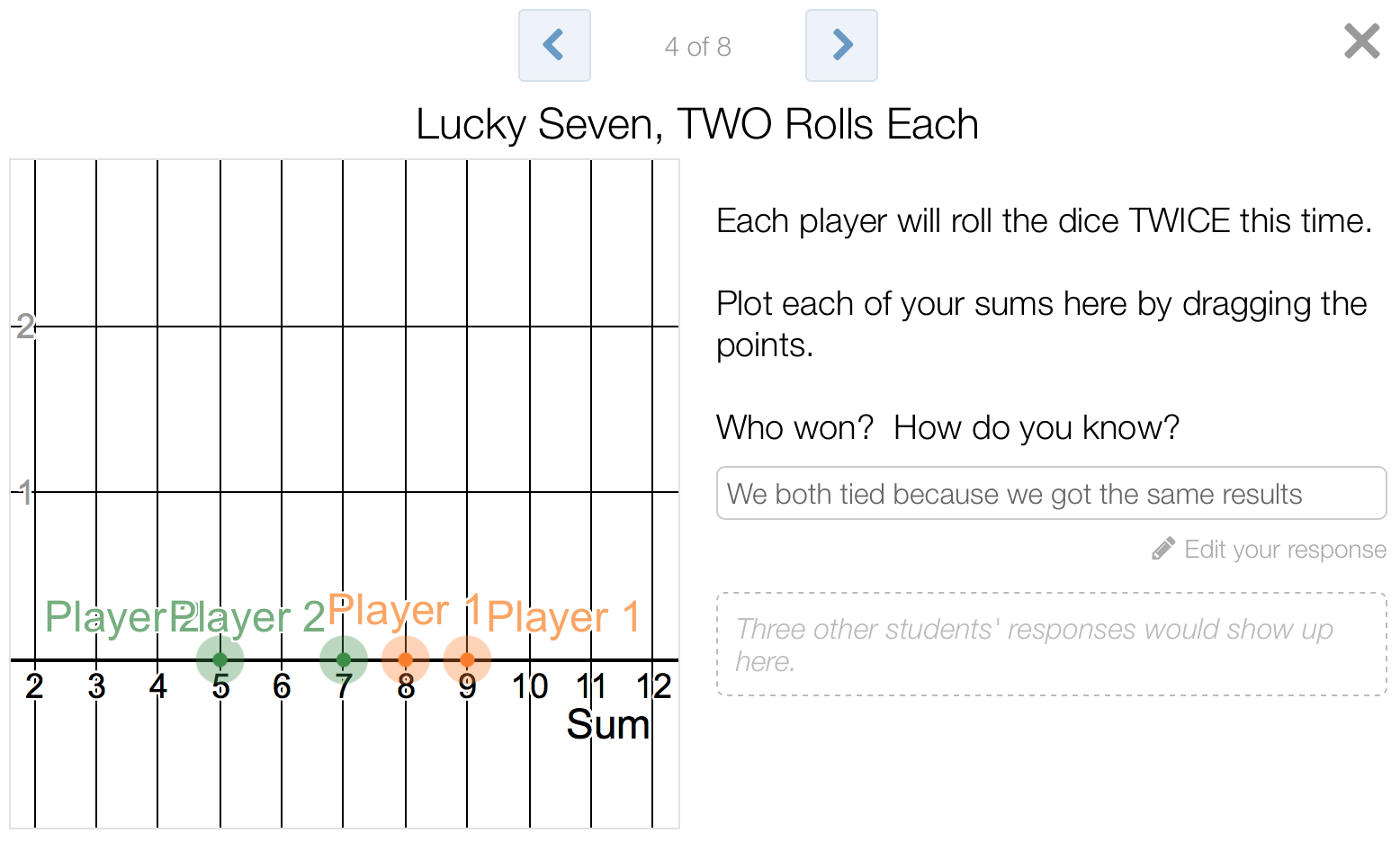
Next, it was time to transition from pairs to teams. Students moved to teams of 3-4 students each, and had to “roll” the dice 10 times each, plotting their own sums. I wrote the word “CHAMPS” on the board, and asked each team to write the name of the student who “won” in their group. That winner from each team would advance to a class tournament from which an entire Sum Game class champion would be established.
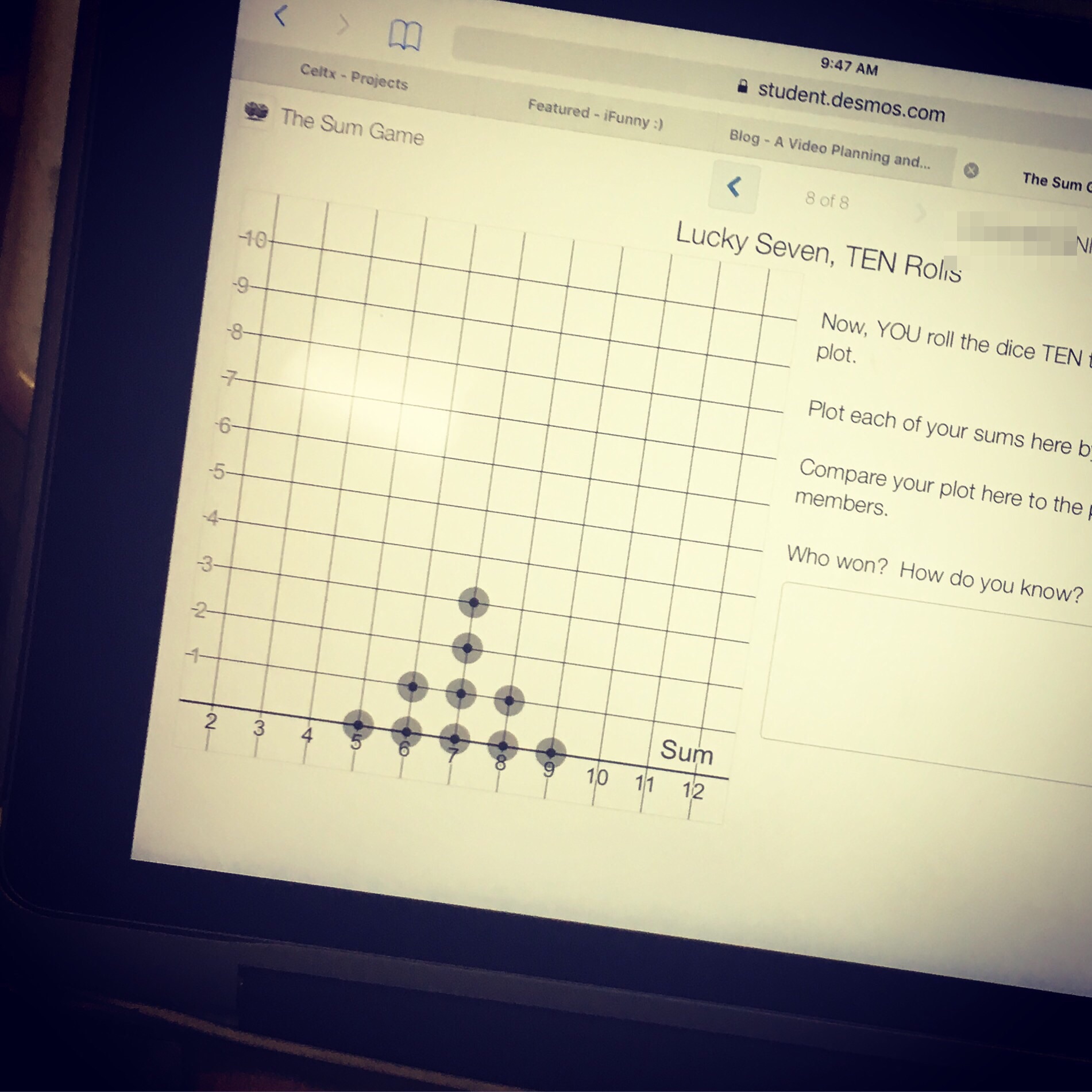
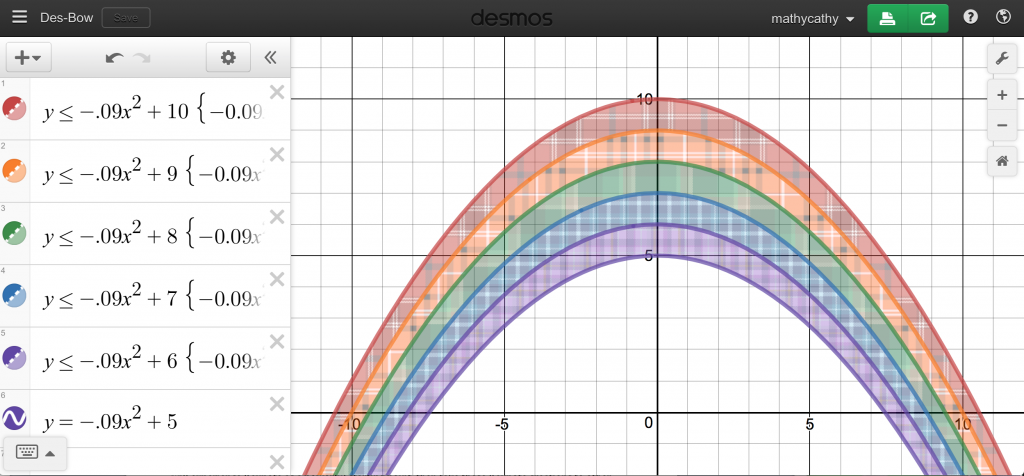
MAD Symmetry!
“Teacher-paced gates” gave students access to screens 7 and 8, and off they went. There was gnashing of teeth when a student rolled a sum of 2 or 12, and eruptions of joy with sums of 7. Once the first team wrote the name of a “champ” on the board, I dramatically interrupted class and said, “Oh! I almost forgot! When you write the name of your team champ on the board, will you also write their score? Thanks!” At first, this request seemed totally reasonable. Then students started declaring winners, walking up to the board, and looked to me for guidance…
“Are we adding them up?”
“Should I write the average?”
“Can I just write how many times our winner rolled a 7?”
“How do I write the score? Can you just tell us?”
My lovely, lovely students. You know me better than this. 🙂

Student teams started to compare strategies for finding “a score” for their winners. One class started the trend of simply writing down how many 7’s each “champ” got, and that was that. We were suspicious… did we really have a three-way tie? Seemed unlikely… so we took a closer look at their line plots to see what the non-7’s were.
Then, it happened. A couple of students erupted with the idea that every 7 should actually be worth 0  points… and that 6 and 8 should each be worth 1 point. I couldn’t write what they were saying fast enough. The class seemed to buy into this idea, and all of a sudden, groups were questioning the champs’ names that were on the board. Kids started yelling (in a good way), “I *KNEW* I won! My name belongs up there!” Everyone feverishly worked their own plots AGAIN, and we started seeing values next to the names of the champs that represented the average of the distances from 7.
points… and that 6 and 8 should each be worth 1 point. I couldn’t write what they were saying fast enough. The class seemed to buy into this idea, and all of a sudden, groups were questioning the champs’ names that were on the board. Kids started yelling (in a good way), “I *KNEW* I won! My name belongs up there!” Everyone feverishly worked their own plots AGAIN, and we started seeing values next to the names of the champs that represented the average of the distances from 7.
I feel like we established important concepts to prepare for the MAD. What transition would you include (in the Desmos activity or otherwise) to bridge this experience to calculating the MAD?
Each class had a “champ” today, but the real win was the entire experience. Thanks again to Nathan for sharing so my students could play “The Sum Game” today! If your students “play” too, I’d love to hear how it goes, and any feedback on tweaks you made to the lesson that worked well with your students!


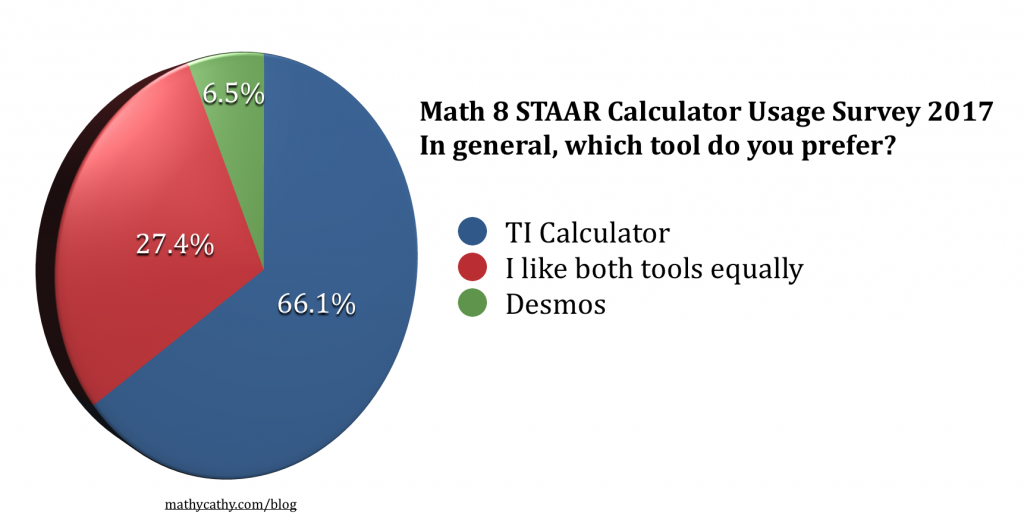
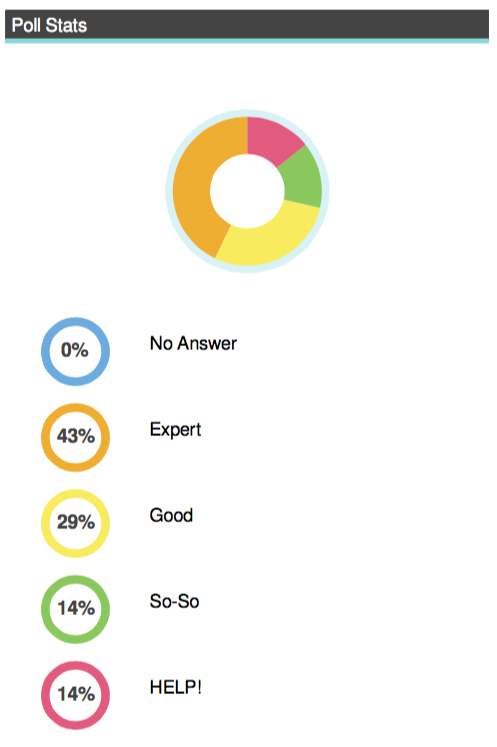
 This week, our Algebra 1 students took their STAAR End-of-Course exam. This round marks year 2 of Algebra 1 students being permitted to use both a TI handheld graphing calculator and the Desmos Test Mode iPad app in light of this TEA calculator policy change that went into effect last school year.
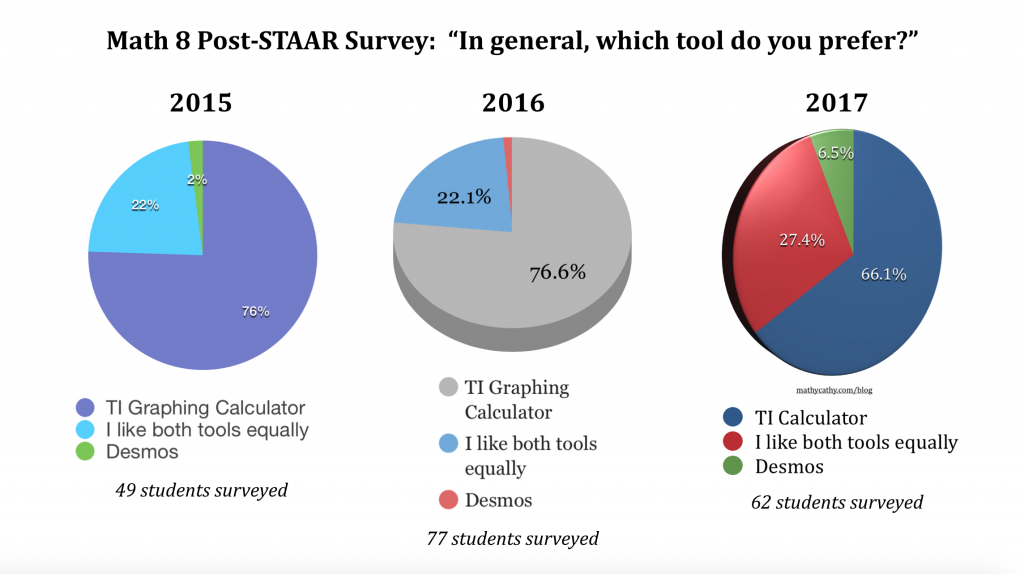
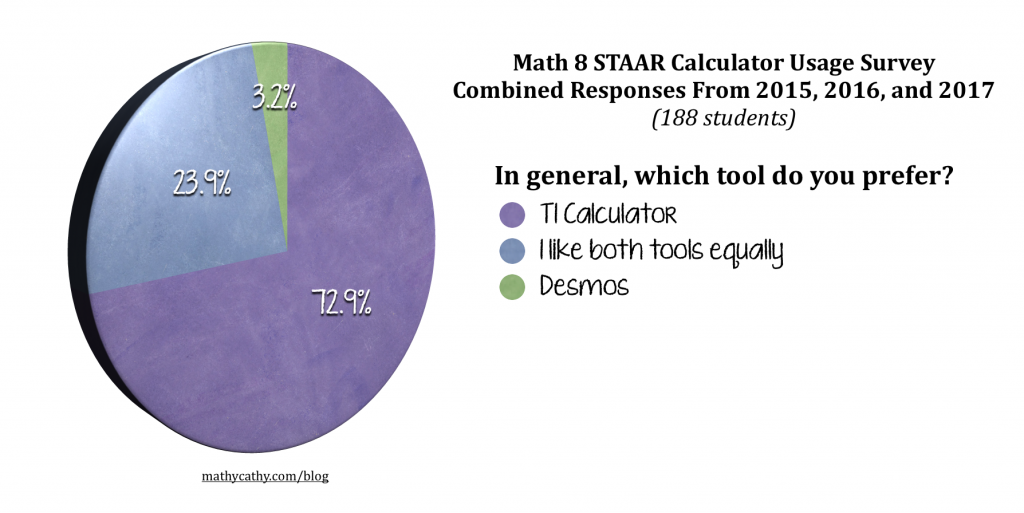
This week, our Algebra 1 students took their STAAR End-of-Course exam. This round marks year 2 of Algebra 1 students being permitted to use both a TI handheld graphing calculator and the Desmos Test Mode iPad app in light of this TEA calculator policy change that went into effect last school year.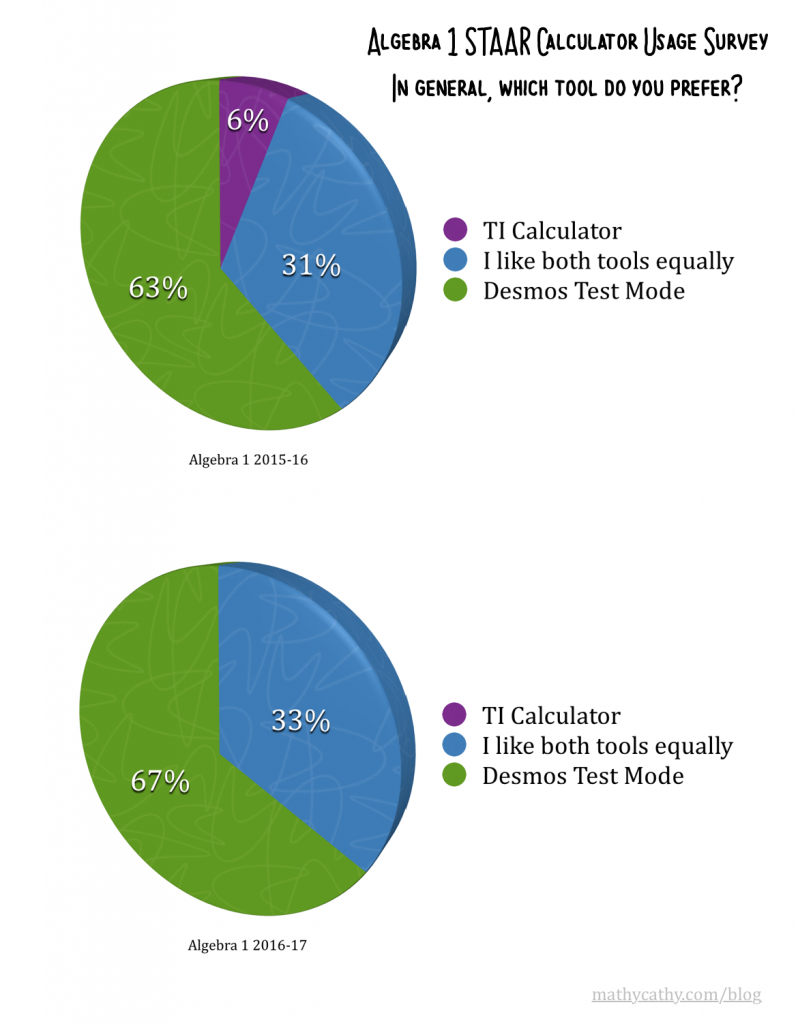 Here’s a side-by-side comparison of this year’s Algebra students and last year’s sample size of 49 students. Additionally, you can check out the unedited and anonymous responses from this year’s Algebra 1 students regarding their favorite concepts to explore using each calculator.
Here’s a side-by-side comparison of this year’s Algebra students and last year’s sample size of 49 students. Additionally, you can check out the unedited and anonymous responses from this year’s Algebra 1 students regarding their favorite concepts to explore using each calculator.