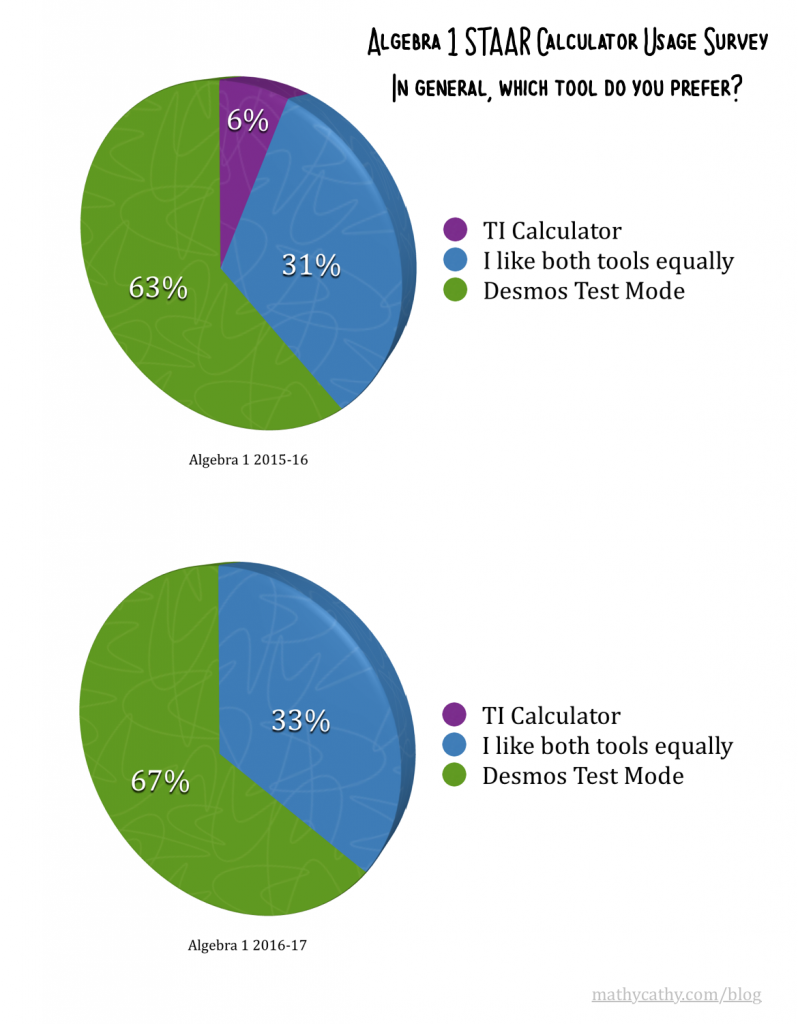
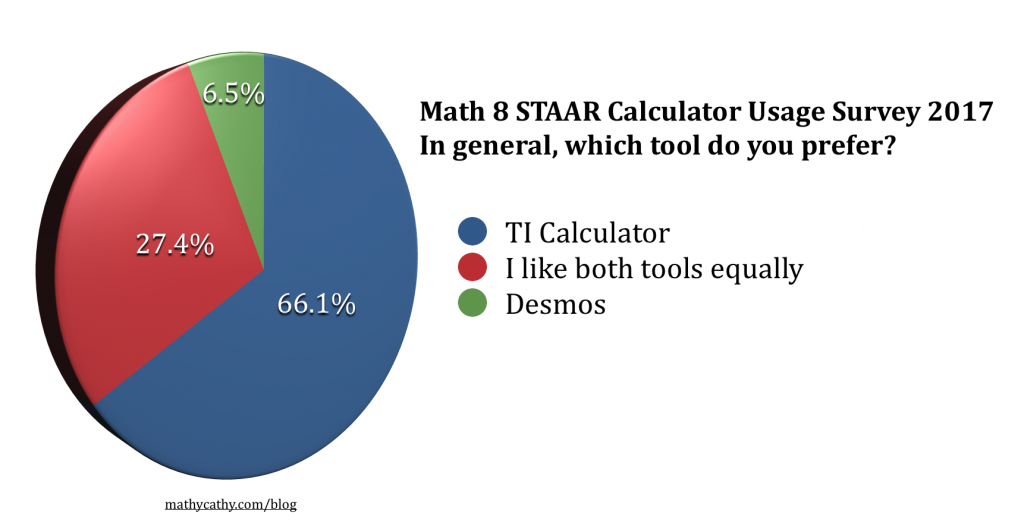
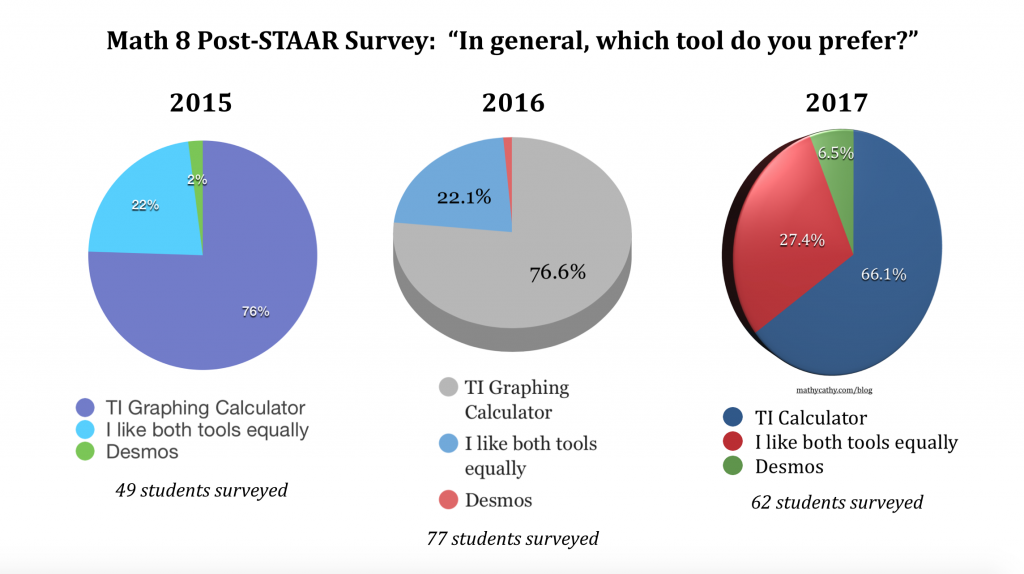
The funny thing about teaching kids is that, every year, they show up, still 12-14 years old. It’s easy to forget that, while they show up the SAME age each year, I am indeed an entire year older than I was the year before. Another funny thing about teaching middle school is how students can keep ya feeling young! I mean, where would I be today without water-bottle-flipping and fidget spinners? 🙂
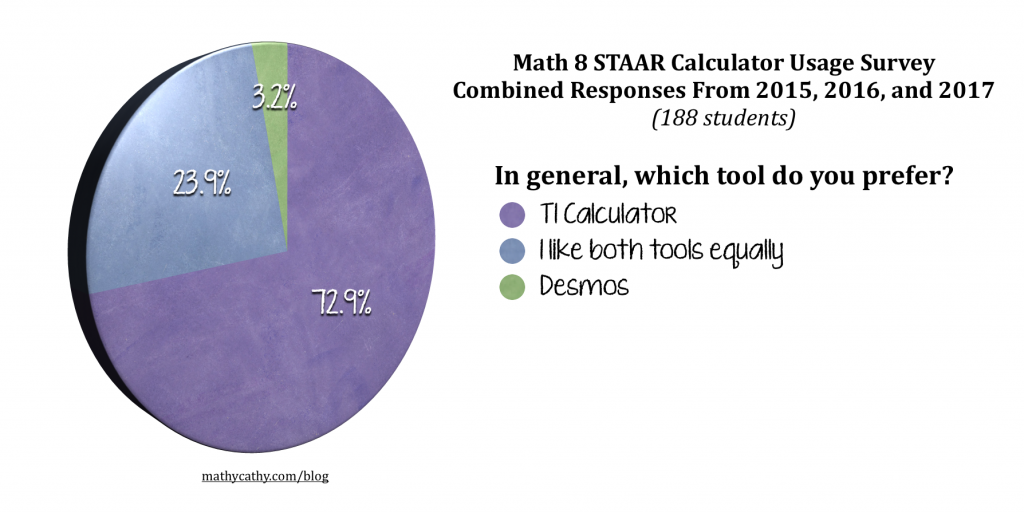
In keeping with tradition, on one of the last days of class, I gave my students the Matt-Vaudrey-inspired Teacher Report Card/Google Form (go here, and scroll ALLLLL the way down to grab it). Students never disappoint in the honesty department. Be brave – ask your kids to grade you, and you’ll get some heart-warming and heart-wrenching feedback. Some of the feedback might leave you feeling like you’re not sure what to do with it… like the kiddos who say SLOW DOWN when other kids say SPEED UP! Or, I love your personality versus, you’re kind of loud sometimes… Nevertheless, taking students’ pulse and considering their feedback is something I brace myself for annually, but I am always, always glad I asked. (Note: I also created a word cloud of things students thought should be improved, but all of those words out of context made no sense. I don’t want to imply that students didn’t also have feedback that was constructive, because they did!)

Celebrity guests offering best wishes to our Hill Country Cougars in my annual Animoto End-of-Year Celebration video montage

That moment when Nathan Kraft’s video message shows up completely unexpectedly! Do you think they were excited?!?
Another tradition I’m so glad I do, because I’m essentially designing a video-yearbook archive of my classes of students each year, is creating an end-of-year celebration video using Animoto. Animoto is one of the easiest tools I know of that merges photos, video clips, text, impressive transitions, and music to create memorable montages.
While I had plenty of media of my students, I added a twist this year – I reached out to some “celebrities” who have become “household names” in my classroom, and invited them each to record themselves wishing my students well in brief personalized videos.
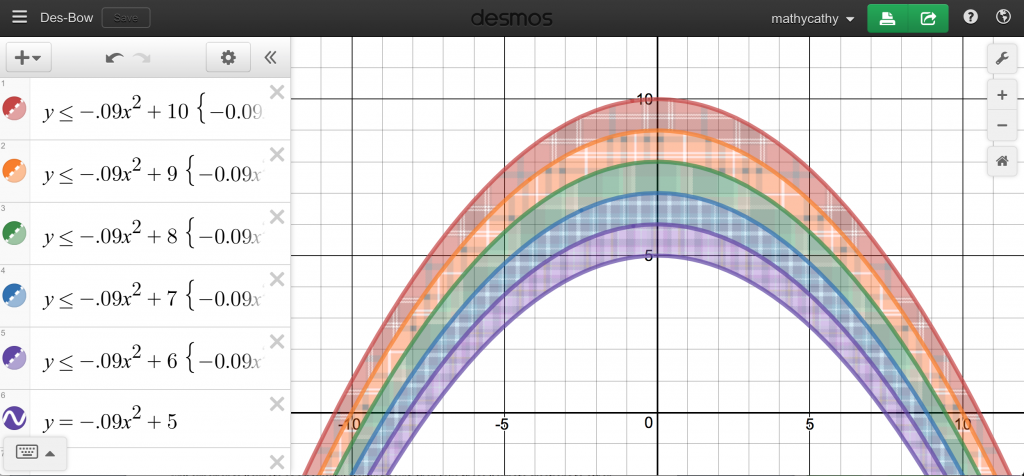
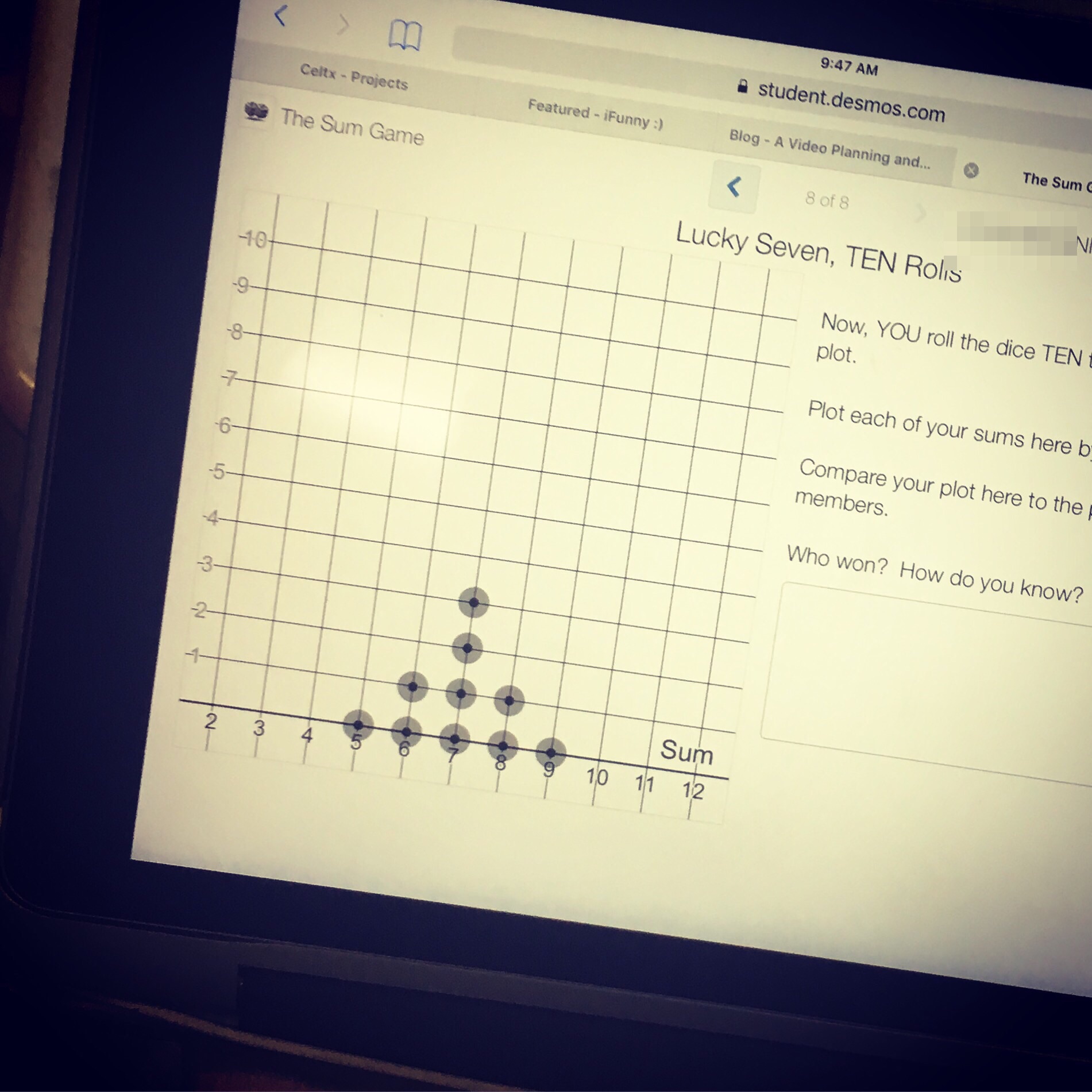
Jamie Brooker (Kahoot!), Guido Kovalskys (Nearpod), Nathan Kraft (the famous “man” that showed up in this Desmos activity screen 7, and henceforth became one class’s mascot for the year), and Eli Luberoff (Desmos) each recorded a message for me to share with my students. I couldn’t be more thankful that each of these fellas played along with my crazy idea – my students felt SO SPECIAL and couldn’t believe that these important people took the time to send them such kind, personal messages!
And then today, I hear from Jen McAleer that some of her students have created t-shirts sporting their own artistic impersonation of… me!
Who knew that the Math-Twitter-Blog-O-Sphere community would extend to our students in this “celebrity” way?!?
I think it’s darling. I also think it proves that we truly never know the extent of our impact! Here’s to another awesome year in the books.
So, who else is done with school, and is already thinking about planning for next year? 🙂
P.S. I stumbled upon this added bonus today on the NCTM Facebook page. It gave me warm fuzzies to think back to #ShadowCon17.
*UPDATE*
Jen McAleer’s students created an impressive end-of-the-year video project, and elected me to be “Math President” for my instructional role in it! It’s not every day you win an election like that! 😉
That moment when @jennifuhs4‘s Ss elect you “math president”, write a script, & invite you to teach in their end-of-year project vid! Fun! pic.twitter.com/3JCupB3Zjq
— Cathy Yenca (@mathycathy) June 20, 2017