It’s my pleasure to have the opportunity to share on NCTM’S Mathematics Teaching in the Middle School “Blogarithm” blog! Check out the first post of four using the link below.
A special thanks to Dr. Clayton Edwards for the opportunity!
Yenca, The Dan, Nadine Herbst, The Fenton
I’m still in that mushy state between being on break and being back to school. An opportunity that helped firm up a few brain cells for me this week was a day with Team Desmos a la Dan Meyer and Michael Fenton.
My biggest take-away (and one that may help others free their minds) was this (paraphrased) proposition from Dan:
What can we (math teachers) do/present/provide for our students before *we* start talking/telling them something?
Simple, right? Profound, right? Now #WCYDWT?
To add a follow-up to this thought, I consider this question:
What can we (math teachers) do/present/provide for our students to monitor their progress right now?
Create the intellectual need somehow. Guide and teach. Then, do a check-in to be sure we’re okay… and if we’re not, know that, and act, involving the kids in the process at every step. This is where I feel so passionately that technology can empower us.
In chatting with teachers, whether it be about Nearpod, Desmos, or (insert tech-tool-du-jour-here), folks sometimes shy away from using tools because creating something seems too overwhelming. We don’t have time. We open a blank Nearpod/Desmos Activity Builder/Socrative quiz, stare at the screen, and close it back up. Maybe we start creating a “lesson” and get frustrated, or think it’s not “good enough” so we drop it.
The saddest part about when this happens is *not* that folks aren’t “integrating technology”. Rather, it’s about a missed opportunity to examine student thinking. To give them a voice during instruction. To see their work and share it with them so *they* can have a mathematical metacognitive moment.
My suggestion – free your mind of expectations regarding how elaborate the activity has to be. Does it *HAVE* to be an entire lesson? Does it *HAVE* to be overly-aesthetically pleasing? Does it *HAVE* to be comprehensive? “Perfect”? Kate Nowak’s nudge this week got me thinking too.
What if a Desmos Activity has only one or two graphing slides with a little something for students to do?
What if a Socrative “quiz” simply asks one or two open-ended questions using Teacher-Paced mode so discussions can ensue?
What if a Nearpod lesson really isn’t a lesson at all, but asks students to work one problem? Draw something? Answer one or two poll or quiz questions?
You see, no one out there is saying, when you create content for your kids, that it has to fill the entire class period. Tech activities don’t have to be stand-alone… that’s why kids need you… remember? 🙂
Here are two such “activities” I’ve designed this week.
Systems of Linear Inequalities Quick Check – Desmos Activity Builder (2 graphing slides)
Today, my Algebra 1 students spent at most 3 minutes here. Using the Overlay feature showed a nice sampling of student thinking. It’s not fancy, profound, or comprehensive, but by watching the points dance around, I know some students learned something… especially those who misplaced the points at first, saw what the class was up to, and corrected a ‘whoops’.
Nearpod Linear Systems by Graphing Learning Check (2 Draw-It graphs, 1 Desmos graph, 2 Open-Ended questions)
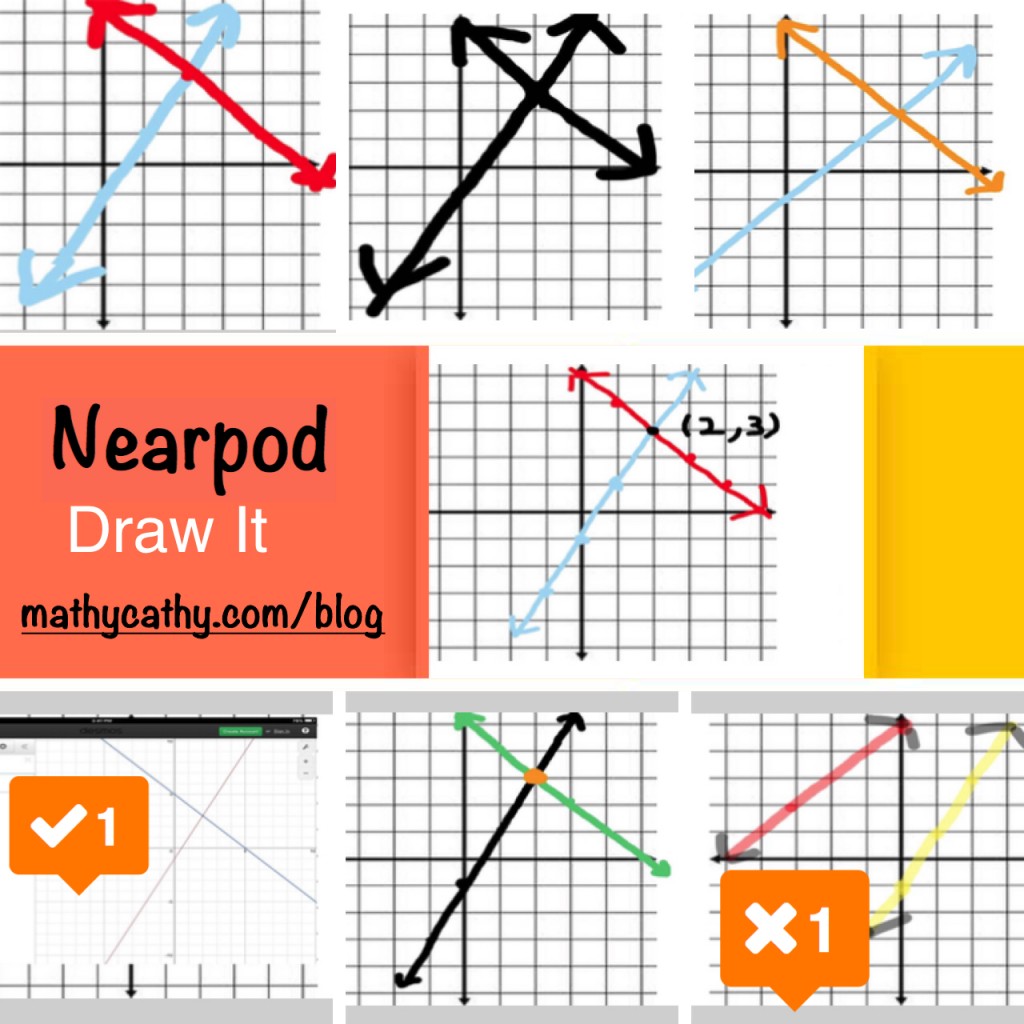Desmos is great for graphing things *for* us. If you want to assess whether *students* can graph an equation by hand, you might need another tool (my suggestion: Nearpod Draw-It. I’m sure you’re surprised.) That’s why I love integrating Desmos and Nearpod to cover all bases.
My Math 8 students spent around 8 minutes on this Nearpod/Desmos mash-up this week. This was my first attempt to embed student.desmos.com into the Nearpod URL tool. That way, I could keep a smooth work-flow between Nearpod Draw-Its AND Desmos Activity Builder (where I could take full-advantage of the Overlay feature without leaving Nearpod… it’s like magic folks.)
Grab this Nearpod lesson. Launch it for students and share the Nearpod PIN with them.
When students get to the Desmos part, they’ll need you to generate a Desmos class code. If you Start a New Session using this link, then share the Desmos class code with them, they’ll be able to do the Desmos activity right in Nearpod, and you’ll be able to project the Overlay feature from the Desmos teacher panel in teacher.desmos.com so kids can see it.
Once the Desmos part is done, advance the Nearpod to present the last two open-ended questions to students. Or, you could throw a poll question here, or any other of Nearpod’s many tools. Magic.
Okay… so maybe that last example was a little more elaborate, but my point is… I tried something new, and I didn’t try to make it my *whole* lesson.
The results were worth it. Student comments when Nearpod and Desmos show up together sound a little something like this. Every time.
“I like this.”
“This should be our lesson every day.”
“Ah, I see what’s going on.”
“I get it now.”
♫ And that’s what it’s all about *clap clap* ♫
The last class or two before Christmas break is a precious time. Students have finished all of their dreaded exams, and they come to class asking,
“Are we going to *DO* anything today?!?”
My answer is usually along the lines of,
“I thought we’d do some math.”
GROAN!!!
As many geometry topics approach us in Math 8, and exponential growth is on the Algebra horizon, the topic of fractals is timely, novel, and welcomed by students, despite their desire to “not do anything”… 🙂
On Day 1, I present the concept of fractal through a “classic” Discovery Education 3-minute video featuring Clifford Pickover. (P.S. You should follow him on Twitter – he tweets the neatest, nerdiest stuff!) Here is another video to introduce the concept of fractals.
Next, I show this video, which features my trip to MOMATH (The Museum of Mathematics) in New York City, and my obsession with the digital fractal exhibit. Yes folks, there were young children in line behind me as I hogged the screen to capture these fun video clips for my students. Totally worth it.
To help students visualize the meaning of “self similarity”, I show about 30 seconds of this video. Trust me, that’s plenty, or everyone gets dizzy!
I think understanding how fractals are built happens best when students draw them by hand. I show this ambitious video before students make their very own Sierpinskis.
Finally, I distribute rulers and this template from the Fractal Foundation website. Students connect midpoints of “right-side-up” triangles, and we explore the growth pattern, deciding the number of new “right-side-up” triangles at each iteration does NOT model a linear pattern. Exponential it is!
As students begin to sketch their fractals, a sort of therapeutic hush falls on the room. Even though they’re starting to understand that, the more midpoints they connect, the more work they’re creating for themselves for the next iteration, they seem to enjoy it anyway. I begin commissioning students for their fractals so I can build a “tree” on my wall. 27 fractals will do!
Many students beg to take their 2D fractals home, and return the next day with some pretty impressive and intricate additions to our classroom wall-tree.
Day 2
Now that we understand the growth patterns and structures of creating a Sierpinski Triangle fractal, we move on to 3D pop-out cards, which double as a great gift for Grandma! Directions can be found on the Fractal Foundation website. This year, students asked me to create a video so they could practice over break, since the first 3D fractal often comes with a few whoops moments. The more fractal cards you make, the nicer they turn out!
Voila – we’ve created memories that will set the stage for similarity and exponential growth in 2016!
Want to know what your students are thinking? How do you get that thinking out of their heads in a format that you, as their teacher, can view, analyze, and use for instructional decision-making? Do you keep this “visible thinking” to yourself? Do you make decisions based on your own analysis of student thinking without letting students have the chance to view and analyze it too?
In one of my recent verbal-brain-dumps (this usually happens at dinnertime with my ever-listening husband) I spoke an analogy that shapes the way I design and execute lessons:
We’re supposed to look at student thinking so we can make instructional decisions, right? Why should the teacher get to be the one-and-only bearer of that knowledge? My strong belief is that we, teachers, should not keep that knowledge to ourselves.
In this era where digital tools are more accessible than ever, we can see student thinking in so many ways, efficiently, and share that thinking with THEM as well. In the same way that it doesn’t help our students if we do math problems *FOR* them, could it be that doing all of their error analysis *FOR* them could also be detrimental? Or at the very least, promote a missed opportunity for learning?
How do I involve my students in viewing and analyzing their own thinking? Thanks to 1:1 iPads, I have a repertoire of tools from which to choose. Here’s some food for thought:
I learned about a new @Nearpod feature while leading a webinar tonight! Game-changer! Thanks @GuidoNearpod! #ipaded pic.twitter.com/1lKW7Z2lrn
— Cathy Yenca (@mathycathy) December 10, 2015
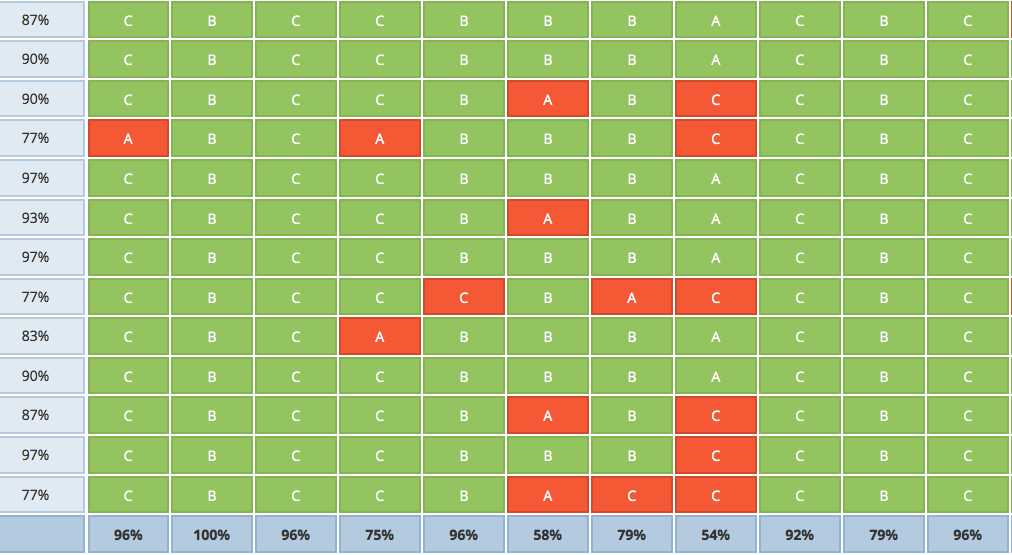
Haven’t used the tools on my shortlist?
Pick one to try in 2016, give it a go, and share back.
It’s the most wonderful time of the year! As the semester winds up (exams!) and then winds down (winter break!) it’s become a good time to give my students some creative opportunities to reflect on what they’ve learned throughout the year.
Last week, my Algebra students wrapped up authoring their own math eBooks in preparation for upcoming semester exams. This is my third lap with this Book Creator project, which is tucked into this iTunes U Course if you want to give it a go with your own students.
If you’d like to read about how this project came to be, check out lap 1 and lap 2 before reading on.
What I did differently this lap:
1. With new Algebra TEKS came new eBook topics. Rather than only providing students with a standard or learning target on which to base their books, I chose this time to give each student group the TEKS/target as well as a representative problem set. Before we even talked about authoring a book, student groups worked together to solve specific problems that varied in difficulty, but were rigorous enough to set clear expectations about the problem-types that would be appropriate for their eBooks. In the past, students often defaulted to too-easy examples. Additionally, some students misunderstood their math topic and wrote books that missed the mark a bit.
2. Each class was provided with exactly three copies of each sample problem set, and I distributed these resources randomly. That meant each student was both assigned a random math topic as well as a random group comprised of exactly three students. Students who mutually agreed to trade papers (and therefore math topics and student groups) were permitted to do so. Some groups of three mutually agreed to become a pair and a lone-ranger, giving rise to multiple books on the same topic. I believe giving students choices helps them own their work, so I remained flexible as they worked through these logistics themselves.
3. This year, I very intentionally framed the project as a “community service project.” The ultimate goal of creating this collection of eBooks was to provide peers with multi-media review resources beyond typical textbooks and worksheets. I think students heard and owned this message. Instead of viewing the eBooks as being a nifty iPad “graded project” with a checklist to complete, students considered their audience, and designed the books with the goal of meeting the needs of their peers.
This is what three days of sub plans looks like. #NCTMregionals #MTBoS
4. Students worked on the majority of this project in my absence! While I was at NCTM Nashville, my amazing sub interviewed each student group daily, and took extensive progress notes for me. Even though I missed seeing a lot of the process in person, I felt very connected to students’ progress through these notes!
Every year, I see the quality of these eBooks improve! Student tutorial videos were the best yet, and most student groups took my advice and included a problem set as a self-checking “quiz” at the end of their books. With emphasis on sound mathematics for meeting the needs of the intended audience (their friends!) I was proud of their work… and so were they!
Here is a ThingLink housing the .ePub files for the eBooks thus far. Missing books are being revised and resubmitted, so stay tuned!
My brain is still on overload from the NCTM Regional Conference in Nashville. I can’t count how many times I engaged with Twitter/blogger faces in 3D whom I’ve respected virtually since I learned about this Twitter/blog thang. What a thrill to connect and learn from each other in person.
Add to this thrill, having the opportunity to help new-to-Twitter folks at the #MTBoS (Math-Twitter-Blog-o-Sphere) booth in the exhibit hall as well as in Twitter-themed sessions. Watching the A-Ha sparkle in the eyes of folks as they signed up for Twitter and entered the #NCTMregionals and/or #MTBoS hashtag(s) for the first time was… awesome! Once your eyes are open to this parallel Twitter-math universe, you just can’t look away.
Come visit the #MTBoS booth at the TN #NCTMregionals. @gfletchy did a great job setting it up. pic.twitter.com/m9io7EymqF
— Andrew Stadel (@mr_stadel) November 18, 2015
When I was invited to be part of the opening keynote session nearly a year ago, I think I turned my head to the left and the right and asked, “Who… me?” To be counted among the likes of Graham Fletcher, Robert Kaplinsky, Laila Nur, and Andrew Stadel was an honor I can’t really articulate. Add to that being valued as a 5-person team by the hugely respected organization that NCTM has been throughout our careers and well… I’m just blown away that I had this opportunity is all. “Thank you” falls short… but… thank you. (Catch the HOMEWORK I assigned in my portion of the keynote, as well as a recording of the entire opening session thanks to Mike Flynn here.)
So many take-aways to share… but I’ll try to be concise here and focus on three biggies (to me).
(1) Teaching lessons that are problem-based is a good thing. If I had a dollar for every time I heard “3 Acts” or “Dan Meyer” I would have walked away from this conference with a killing. I really wish I would have kept a tally. From Graham Fletcher and Michael Wiernicki’s Apple-Cube-Balance task, to Robert Kapinsky’s In-N-Out Burger task, to Andrew Stadel’s Swing-Wrapping task, to Dane Ehert’s Elevator-or-Stairs task (and these are sessions I went to – I’m sure there were more!) the message was both consistent and clear:
(2) Teachers I spoke with aren’t doing “3 Acts” EVERY LESSON, EVERY DAY. I think it’s important to address “mathematics in real-life” from the perspective of math TEACHERS. I had more than one conversation with folks who are trying to implement problem-based tasks such as “3 Acts” structures and strategies. We had some keeping-it-real discussions about how often and how successfully we’ve implemented these tasks, and my conclusion is this – not one of us has this type of thing mastered yet. We’ve had some great student experiences, and others that fell flat. We’re willing, but not always able, to execute as we’d like. One colleague went so far as to say, “You’d be disappointed if you came to my classroom” because of the “traditional” teaching that often happens. Another teacher pal said, without any self-condemnation, “I still do a lot of traditional things in my classroom as well.”
In “real” classrooms, balance as well as variety seem to be the name of the game.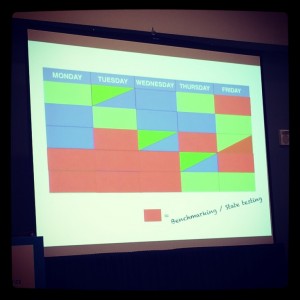 
Geoff Krall’s session title, “Fumbling toward Inquiry: Starting Strong in Problem-Based Learning” gave us permission to continue to grow in this type of teaching while acknowledging “real-life” teacher challenges. This colorful slide from Geoff’s session gave me some #MTBoS Affirmation that my classroom may resemble that of many of us who want to press forward, with intentionality and variety in our teaching techniques… while functioning within some inevitable structures of public education (namely, time-pressures and high-stakes testing, both at the state and district level).
In this sample planning calendar slide, BLUE days signify direct instruction, GREEN days signify problem-based lessons, and those RED days… you guessed it… benchmarking/state testing days. To me, Geoff showed this slide with equal doses of reality and tongue-in-cheek humor, but I found a strange comfort in his acknowledging these challenges nonetheless.
Robert Kaplinsky explicitly stated in his session that doing 1 or 2 tasks per unit can be a “sweet spot” and starting a unit with a task can be particularly powerful. Robert also said (I’m paraphrasing here, but not by much) that he’d rather we “suck” at implementing a task that has already been tested and vetted BEFORE being shared freely in the blog-o-sphere than “sucking” at a task we may have put together from scratch that (we may not realize) begins with a “sucky” problem that was doomed from the start. I appreciated this advice tremendously, and I think it’s worth sharing with colleagues who may take their first stabs at tasks like this… because developing “good” ones, as Robert said, can take a “long-a$$-time.”
(3) Real-life in-person interactions strengthen our virtual-professional relationships.
I met SO MANY PEOPLE whose work I respect and who have inspired me in so many ways. Talking in person only grows that connection. I wouldn’t hesitate to reach out to any one of the #MTBoS members I had the pleasure of getting to know better this week. The SINCERITY of our passions and desires to improve and bring others along on the journey was undeniable. A shout-out to my roomie Laila Nur for refreshing conversations about instruction, standards-based grading, leadership, and life! So glad to have connected with you! Additionally, it was great fun to find out just how alike we are (in pretty much every way) Julie Reulbach!
I’ll admit it… meeting Tweeps in person left me a little star-struck more than once 🙂 but the truth is we’re all normal people with genuine hearts for teaching math and serving our students better. Getting there requires all of us to continue to work together… because the smartest person in the #MTBoS… IS the #MTBoS.
That being said… though we have the #MTBoS at our fingertips 24-7, there is tremendous value in bringing people together for math-fellowship in person. Are you attending professional conferences? Will we meet at a future NCTM? I hope so!
Want to read more about #NCTMregionals Nashville? Check out this reflective post by Tracy Zager. Here’s another follow-up reflection from Jonathan Schoolcraft.
See you in the Math-Twitter-Blog-o-Sphere.
Sessions I attended at #NCTMregionals Nashville:
My students “discovered” slope-intercept form in class last Friday through a paper-pencil graphing exploration that had just the right frustration level to get them talking, exploring, and revising until they “got it”. While we didn’t have a lot of time to come back together and formalize y = mx + b on Friday, I felt like they’d done enough to tackle Michael Fenton’s “Match My Line” today. Last year, my students accessed each Desmos graphing task from a ThingLink. This year, with the birth of Desmos Activity Builder, students tackled each challenge with a smoother living-in-Desmos work-flow.
Before we visited student.desmos.com, I gave a brief assessment using ThatQuiz to be sure we all remembered last Friday’s discoveries. Initially, I had planned to use “Match My Line” and then let students play a linear “Polygraph” activity… but we never got to the Polygraph.
Did you ever just wish another teacher was in the room with you to witness that this-is-actually-happening kind of lesson? That was today! After circulating with a goofy grin on my face for longer than I should have, I had the sense to grab a notepad and jot down some student comments I heard as they worked. I lost count of how many times students threw both hands up in the air as they said these, and many other comments, out loud:
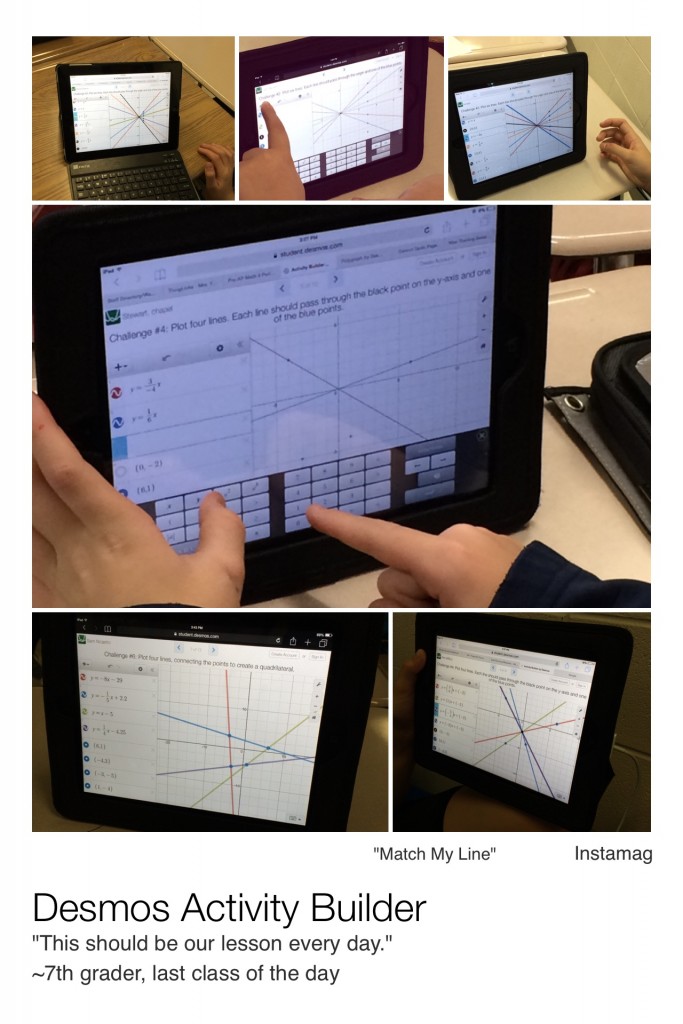“See?!? I’m smart!”
“I didn’t know we could use decimals!”
“I GOT IT!!! I GOT IT!!!”
“… I missed it!”
“I’m almost done – I feel so smart right now.”
“Got it! Perfect!”
“OH! I did it wrong!”
“This is making me SO MAD… wait… BANG! GOT IT!”
and my favorite… as the bell was ringing to dismiss for the day…
“This should be our lesson every day.”
Has it ever been so simple to create and share interactive math lessons that rock? The Desmos Activity Builder is inspiring math educators all over to take lesson ideas to new levels. Head on over to Twitter and search for @Desmos and/or #ActivityBuilder… and you might just bump into exactly what you’re looking for… or at the very least, something BETTER than what you’ve done before!
I recently used this Dilations activity shared by Andrew Stadel along with my own Dilations Nearpod lesson with students, and that was all it took to get hooked! Inspired by Andrew’s work, I whipped up this Reflections exploration to see what it was like to create my very own Desmos Activity. 
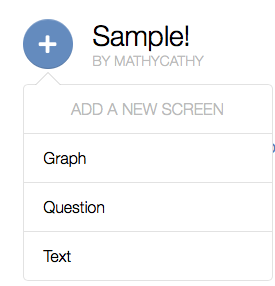It’s quite easy! Go here and select “Start Building an Activity”. The sky’s the limit – mix “Graph”, “Question”, and “Text” options to create a Desmos journey, and share it on Twitter using the #ActivityBuilder and #MTBoS hashtags. You know that lesson topic you dread? Or the one that kids don’t “get” or “see”? Could Activity Builder help? Creativity is key, and let me tell you, there are already quite a few creative people out there making great stuff.
Looking for something specific? Want to share activities you’ve made? You should check out the Desmos Bank. P.S. I can’t wait for my students to experience this activity by Michael Fenton in a new Desmos Activity format!
Have you seen this? I can’t. Stop. Clicking.
Also worth mentioning is this nifty “overlay” option of viewing student work – super cool.
Loving the @desmos overlay feature in Activity Builder tasks – easy to see trends in S work! cc @mr_stadel pic.twitter.com/70LELY1vxw
— Cathy Yenca (@mathycathy) October 26, 2015
#WODB Warm-Up
If you haven’t used Which One Doesn’t Belong? with students, you might be missing out on some pretty awesome dialogue. The idea that there isn’t just one cut-and-dry answer makes justifying one’s choice a safe challenge.
Rookie Mistake…
Students have been solving multi-step equations and had this Nearpod for homework last night. They knew coming in to class today that some equations have no solution and others have infinitely many solutions. Since I already saw their Nearpod HW data and work (which included correct equations as well as typical distributive sign mistakes) we started class with a #WODB Nearpod warm-up to get things rolling. With scrap paper handy and iPads nearby, students worked in pairs to solve the four equations. Going into an activity like this, I think it’s important that students know that there isn’t just one right answer. Simply ask students to take a stand, and be ready to justify the choice.
My favorite part about any task that promotes communication and reasoning is just walking around the room to listen to my students. They take a stand. They change their minds. It’s so tough to choose just one equation! They make mistakes. They try again. And… they know they will be held accountable.
Once students solved the equations and made a choice, they entered their choices and justifications through an Open Ended Response question in Nearpod. I anonymously shared student choices and we talked about each one. A lot of great correct thinking… and quite a bit of great incorrect thinking to straighten out too. Fifteen minutes well spent!
Here’s the quick Nearpod so you can try it out. If you use this #WODB warm-up with your students, I’d love to know how it goes!
Here are just a few student responses from today:
Okay, let’s be clear.
I *DO* teach. A lot.
But students don’t often know how to articulate that *how* I’m trying to teach may differ, at times, from some of their past math-class experiences.
They might not know exactly how to say,
“You teach by having us discover stuff on our own before you just tell us a formula.”
or
“You teach by having us talk to one another and work to be ‘patient problem solvers’ rather than just telling us what to do next.”
or
“You teach by answering our questions with other questions designed to make us think, or to encourage us to test stuff to see if our theory works or falls apart. You don’t own all of the knowledge in this room, and you want us to own it, and not be afraid to make mistakes along the way… because that’s how learning happens.”
or
“You teach by discouraging memorization and ‘tricks’ that really have nothing to do with understanding math, even though I really… REALLY want you to tell me tricks. Deep down, I’m a young learner who just wants you to tell me something that will work, all the time, for every problem.”
“You don’t teach” actually means, “Teacher, you’re doing a great job of being ‘less helpful’. I’m frustrated, but when I put the pieces together and form my own meaning from all of this, I’ll really, REALLY understand it. And I may even thank you for it… but probably not this year.”
I was a bit down in the dumps last week after some student comments like this, accompanied by some test grades that were less-than-desirable. I take it to heart when my students don’t succeed. But I have to remember that they’re still working on it. They’re not there (here comes that ever-important word) YET.
New TEKS (Texas standards), new books, higher expectations… growing pains are inevitable.
But we’ll get there, even if we’re not there… yet.
Thanks to the #MTBoS and particularly my pal Kyle Pearce for encouragement and empowerment to keep pressing on… because I’m not done… yet. We’re just getting started, and we’ll get there!
A timely post from Kyle can be found here:
Tips Moving From Procedures to Understanding in Math Class https://t.co/yIflTEU8E8 #MTBoS #ADEchat #edchat #maths pic.twitter.com/7CtJXtcsJ8
— Kyle Pearce (@MathletePearce) October 3, 2015
