
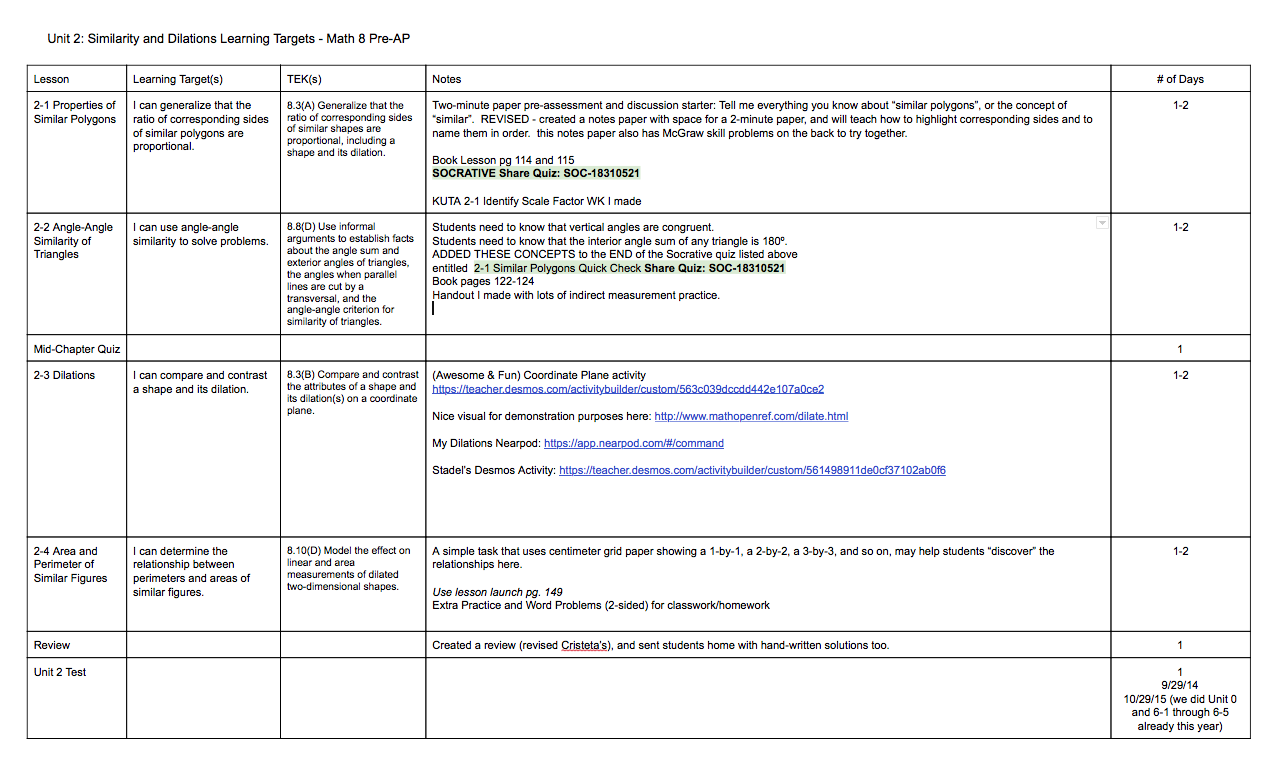
Yenca, The Dan, Nadine Herbst, The Fenton
I’m still in that mushy state between being on break and being back to school. An opportunity that helped firm up a few brain cells for me this week was a day with Team Desmos a la Dan Meyer and Michael Fenton.
My biggest take-away (and one that may help others free their minds) was this (paraphrased) proposition from Dan:
What can we (math teachers) do/present/provide for our students before *we* start talking/telling them something?
Simple, right? Profound, right? Now #WCYDWT?
To add a follow-up to this thought, I consider this question:
What can we (math teachers) do/present/provide for our students to monitor their progress right now?
Create the intellectual need somehow. Guide and teach. Then, do a check-in to be sure we’re okay… and if we’re not, know that, and act, involving the kids in the process at every step. This is where I feel so passionately that technology can empower us.
In chatting with teachers, whether it be about Nearpod, Desmos, or (insert tech-tool-du-jour-here), folks sometimes shy away from using tools because creating something seems too overwhelming. We don’t have time. We open a blank Nearpod/Desmos Activity Builder/Socrative quiz, stare at the screen, and close it back up. Maybe we start creating a “lesson” and get frustrated, or think it’s not “good enough” so we drop it.
The saddest part about when this happens is *not* that folks aren’t “integrating technology”. Rather, it’s about a missed opportunity to examine student thinking. To give them a voice during instruction. To see their work and share it with them so *they* can have a mathematical metacognitive moment.
My suggestion – free your mind of expectations regarding how elaborate the activity has to be. Does it *HAVE* to be an entire lesson? Does it *HAVE* to be overly-aesthetically pleasing? Does it *HAVE* to be comprehensive? “Perfect”? Kate Nowak’s nudge this week got me thinking too.
What if the things we create are small.
What if a Desmos Activity has only one or two graphing slides with a little something for students to do?
What if a Socrative “quiz” simply asks one or two open-ended questions using Teacher-Paced mode so discussions can ensue?
What if a Nearpod lesson really isn’t a lesson at all, but asks students to work one problem? Draw something? Answer one or two poll or quiz questions?
You see, no one out there is saying, when you create content for your kids, that it has to fill the entire class period. Tech activities don’t have to be stand-alone… that’s why kids need you… remember? 🙂
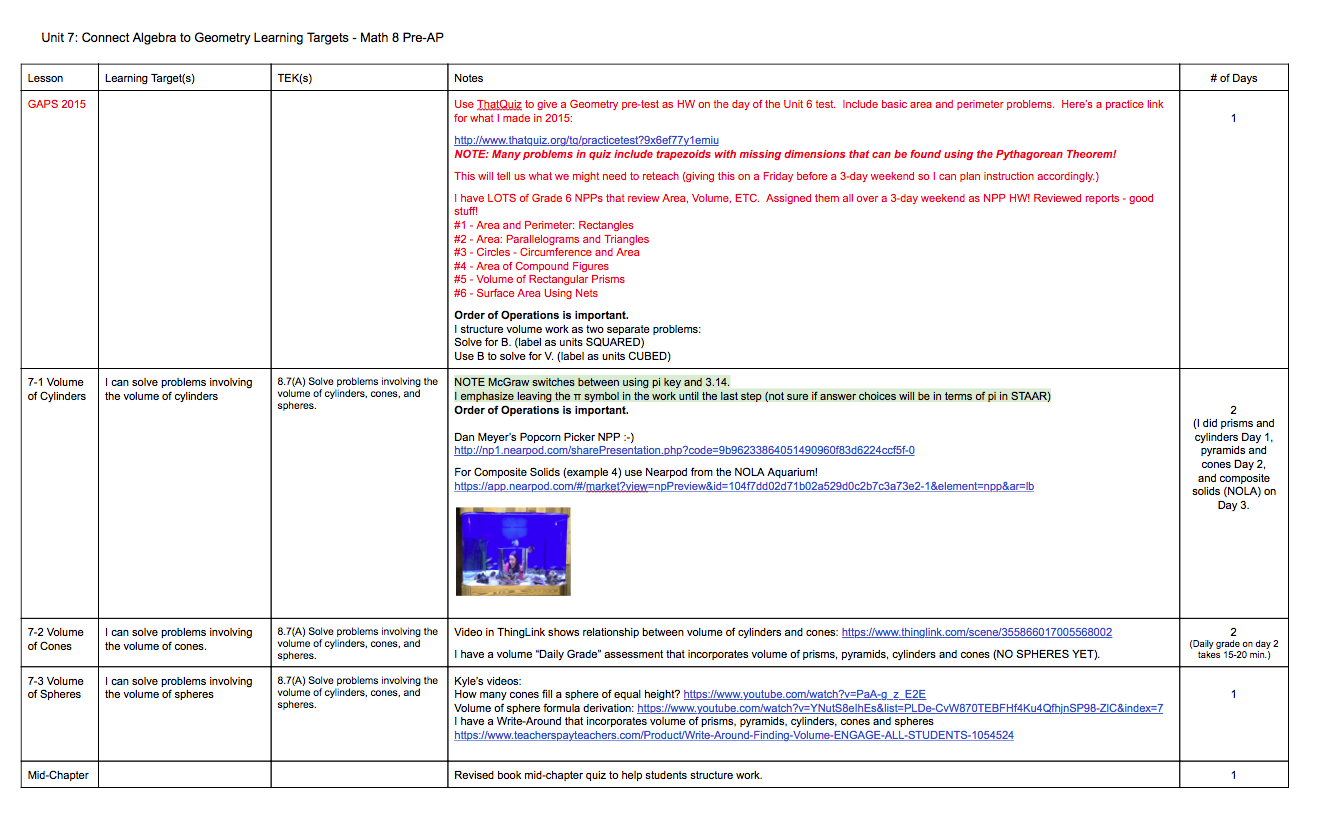
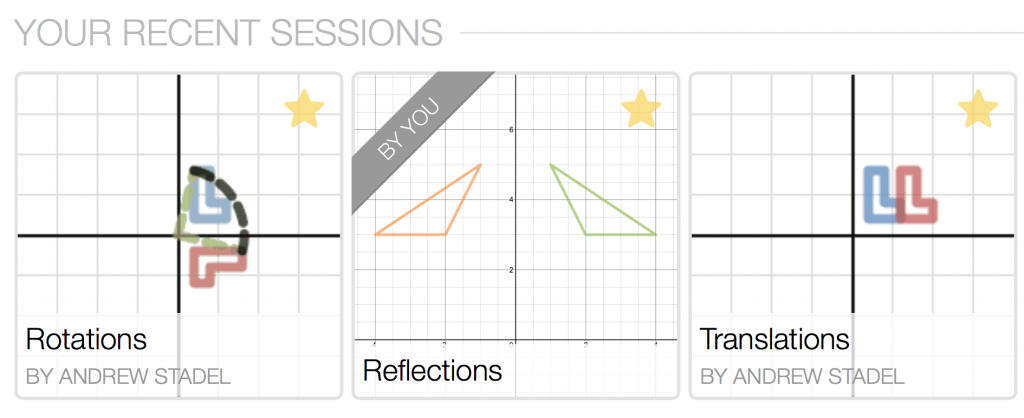
Here are two such “activities” I’ve designed this week.
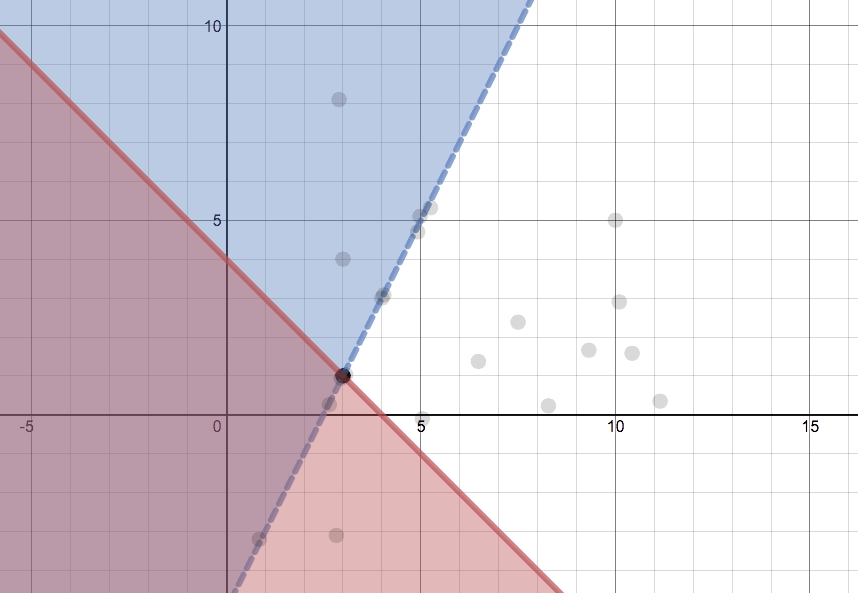
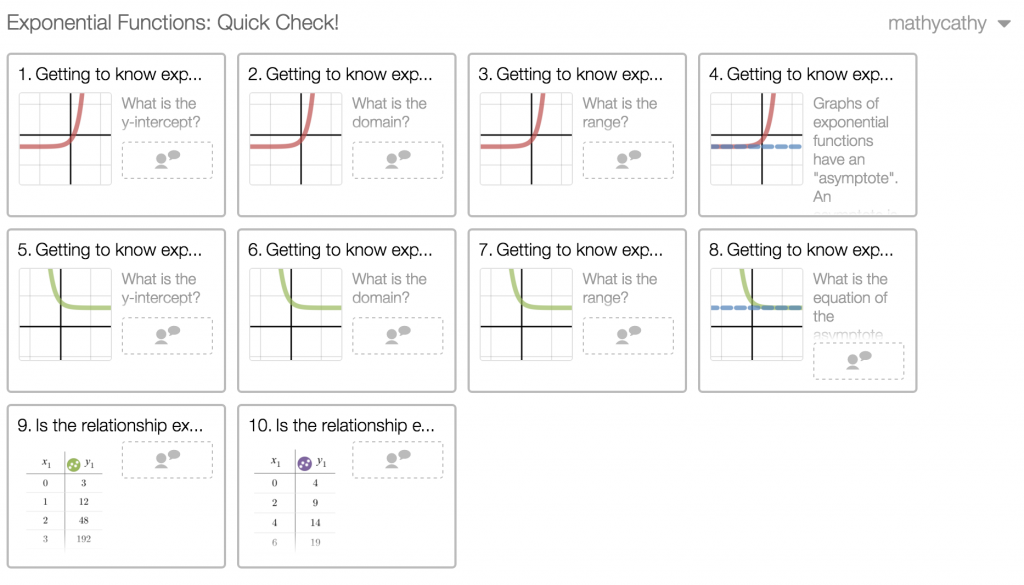
Systems of Linear Inequalities Quick Check – Desmos Activity Builder (2 graphing slides)

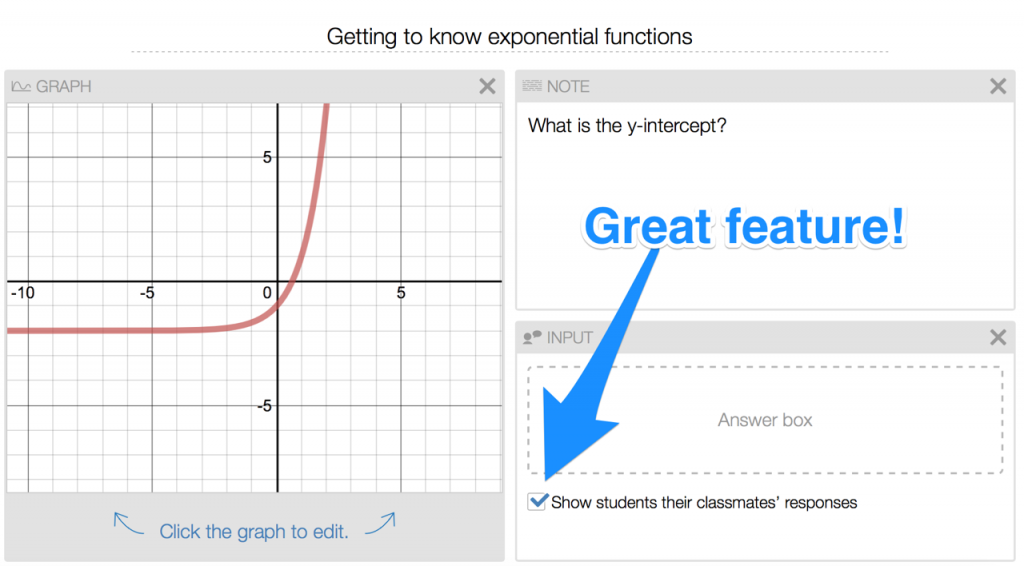
Today, my Algebra 1 students spent at most 3 minutes here. Using the Overlay feature showed a nice sampling of student thinking. It’s not fancy, profound, or comprehensive, but by watching the points dance around, I know some students learned something… especially those who misplaced the points at first, saw what the class was up to, and corrected a ‘whoops’.
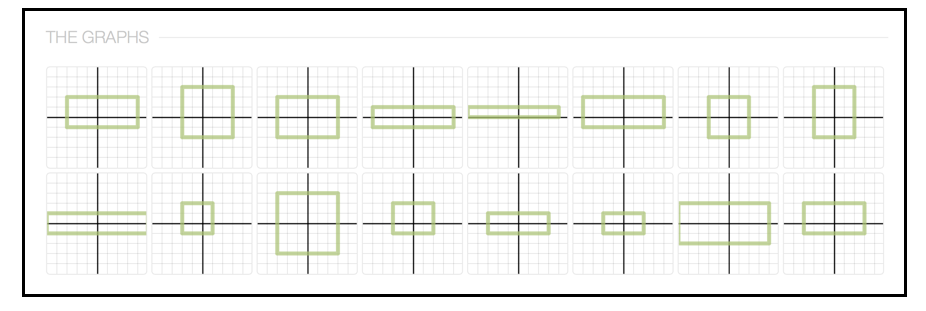
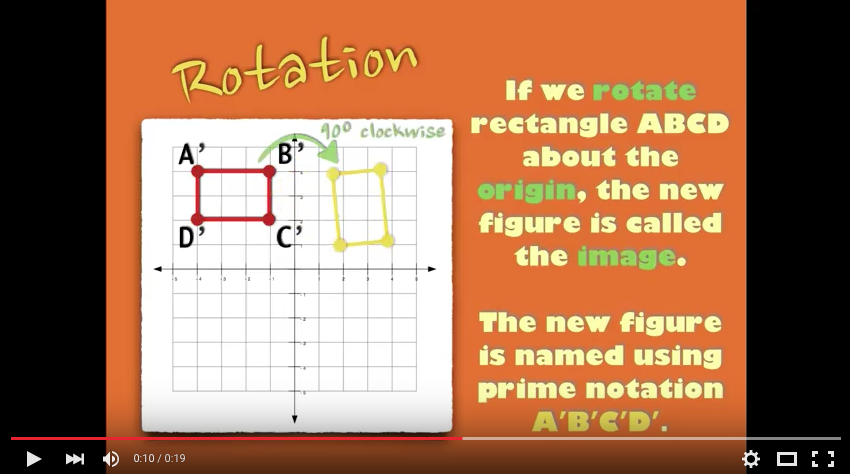
Nearpod Linear Systems by Graphing Learning Check (2 Draw-It graphs, 1 Desmos graph, 2 Open-Ended questions)
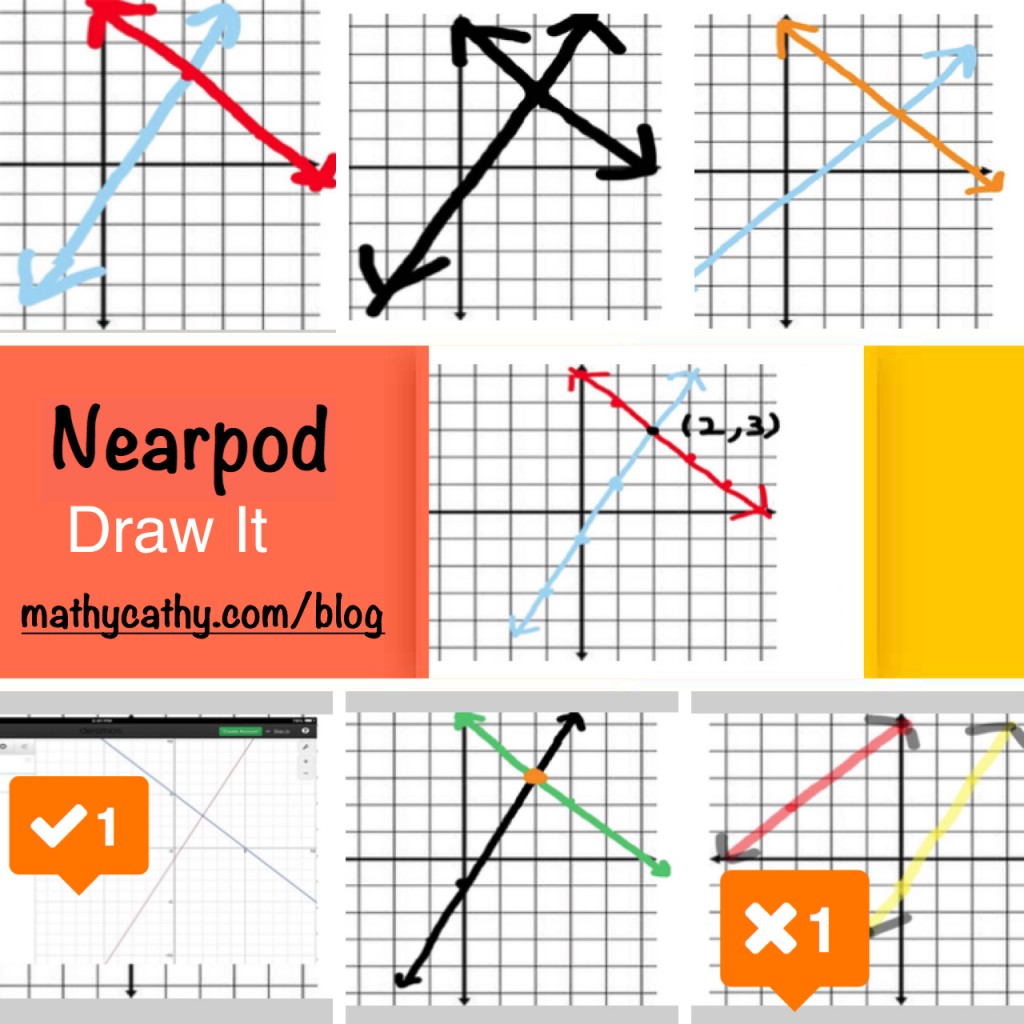 Desmos is great for graphing things *for* us. If you want to assess whether *students* can graph an equation by hand, you might need another tool (my suggestion: Nearpod Draw-It. I’m sure you’re surprised.) That’s why I love integrating Desmos and Nearpod to cover all bases.
Desmos is great for graphing things *for* us. If you want to assess whether *students* can graph an equation by hand, you might need another tool (my suggestion: Nearpod Draw-It. I’m sure you’re surprised.) That’s why I love integrating Desmos and Nearpod to cover all bases.
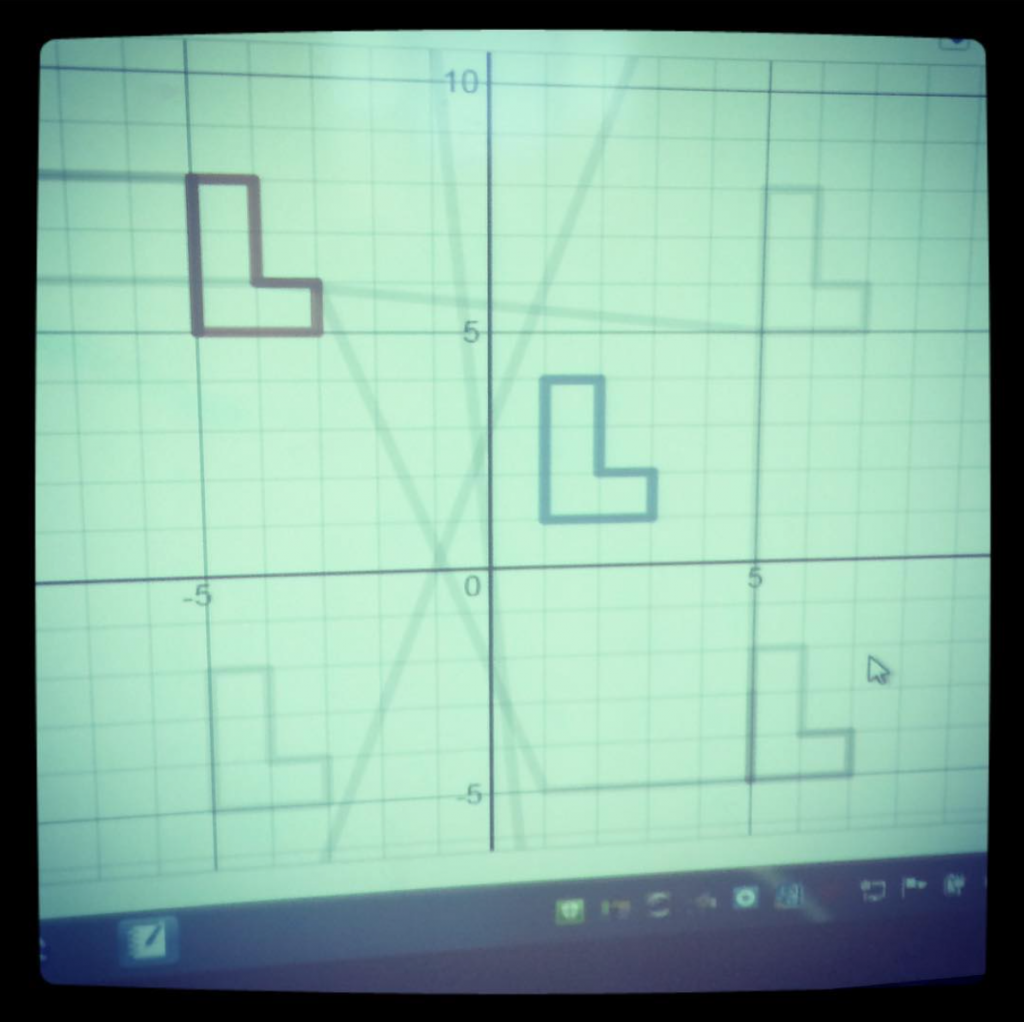
My Math 8 students spent around 8 minutes on this Nearpod/Desmos mash-up this week. This was my first attempt to embed student.desmos.com into the Nearpod URL tool. That way, I could keep a smooth work-flow between Nearpod Draw-Its AND Desmos Activity Builder (where I could take full-advantage of the Overlay feature without leaving Nearpod… it’s like magic folks.)
Grab this Nearpod lesson. Launch it for students and share the Nearpod PIN with them.
When students get to the Desmos part, they’ll need you to generate a Desmos class code. If you Start a New Session using this link, then share the Desmos class code with them, they’ll be able to do the Desmos activity right in Nearpod, and you’ll be able to project the Overlay feature from the Desmos teacher panel in teacher.desmos.com so kids can see it.

 Once the Desmos part is done, advance the Nearpod to present the last two open-ended questions to students. Or, you could throw a poll question here, or any other of Nearpod’s many tools. Magic.
Once the Desmos part is done, advance the Nearpod to present the last two open-ended questions to students. Or, you could throw a poll question here, or any other of Nearpod’s many tools. Magic.
Okay… so maybe that last example was a little more elaborate, but my point is… I tried something new, and I didn’t try to make it my *whole* lesson.
The results were worth it. Student comments when Nearpod and Desmos show up together sound a little something like this. Every time.
“I like this.”
“This should be our lesson every day.”
“Ah, I see what’s going on.”
“I get it now.”
♫ And that’s what it’s all about *clap clap* ♫
SaveSave
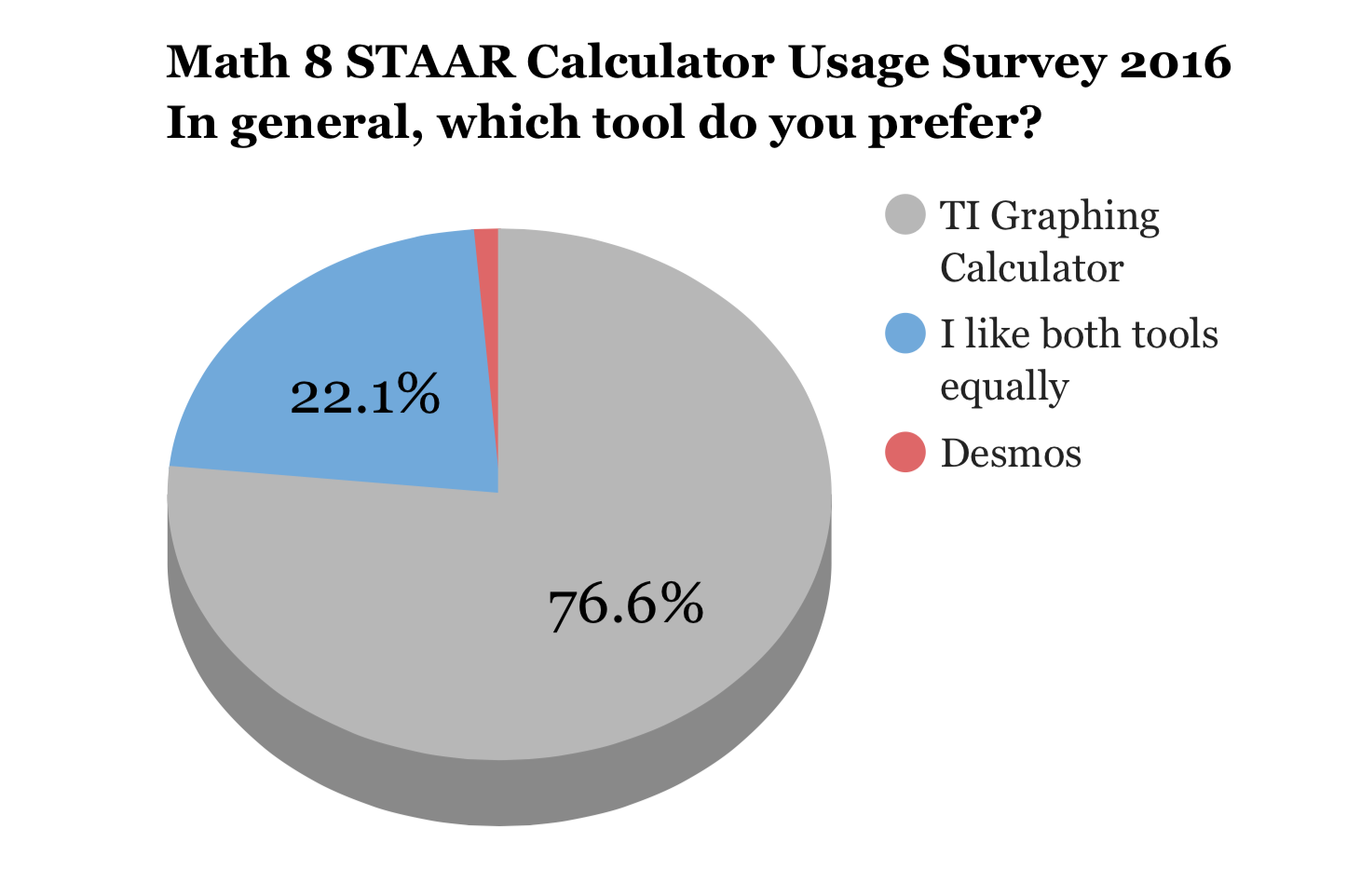
 Last year, our district pioneered using the Desmos Test Mode iOS app on STAAR (state) tests. You can read about that here.
Last year, our district pioneered using the Desmos Test Mode iOS app on STAAR (state) tests. You can read about that here.












 Once the Desmos part is done, advance the Nearpod to present the last two open-ended questions to students. Or, you could throw a poll question here, or any other of Nearpod’s many tools. Magic.
Once the Desmos part is done, advance the Nearpod to present the last two open-ended questions to students. Or, you could throw a poll question here, or any other of Nearpod’s many tools. Magic.





















