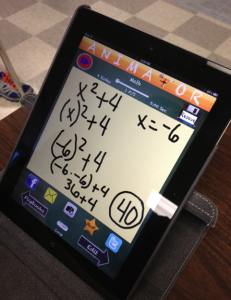Our staff is brand-new to this 1-to-1 iPad gig. We help each other, share ideas, and seek help and feedback from our students. Recently, I heard a broad generalization about our 1-to-1 that irked me…
The statement was that the students “don’t like doing math on the iPad”.

So, I had to investigate – what did this feedback actually mean? I surveyed my students and sure enough, they said they would rather “do math on the iPad” than paper. I asked them where they thought this generalization might be coming from. Upon digging deeper, it wasn’t “doing math” that some disliked – it was the limitations of some of the apps we have been using that left a bad taste in their mouths. Some also admitted that it wasn’t the math itself, but the fact that they hadn’t purchased a stylus yet that made math less-than-delightful on the iPad. Most students have taken care of that issue.

After having this chat, I have been incorporating more PDF files to annotate when appropriate. I have also come to appreciate the DocAS app a LOT. So have my students. DocAS has a neat organization system built right in that some annotating apps currently lack. I taught students how to create an Algebra folder within the app, and move documents into the folder to keep their iPads clutter-free.
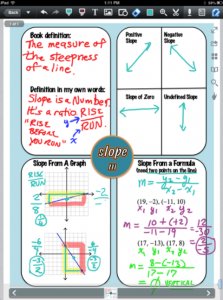
One annotating task that worked well was a graphic organizer on the concept of “slope”. We zoomed in and out of the PDF to tackle one section of the G.O. at a time, as students helped to co-create its contents. You could seriously hear a pin drop as students customized these. It was fun for me to pause and watch them work. No one could argue that every single student was engaged. I asked, “How many of you would have preferred a paper copy for this task?” No hands went up, but I got some very weird “are-you-kidding-me?” looks! 😉
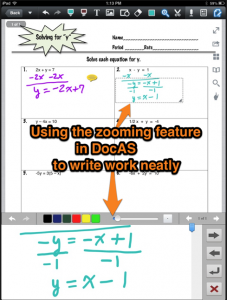
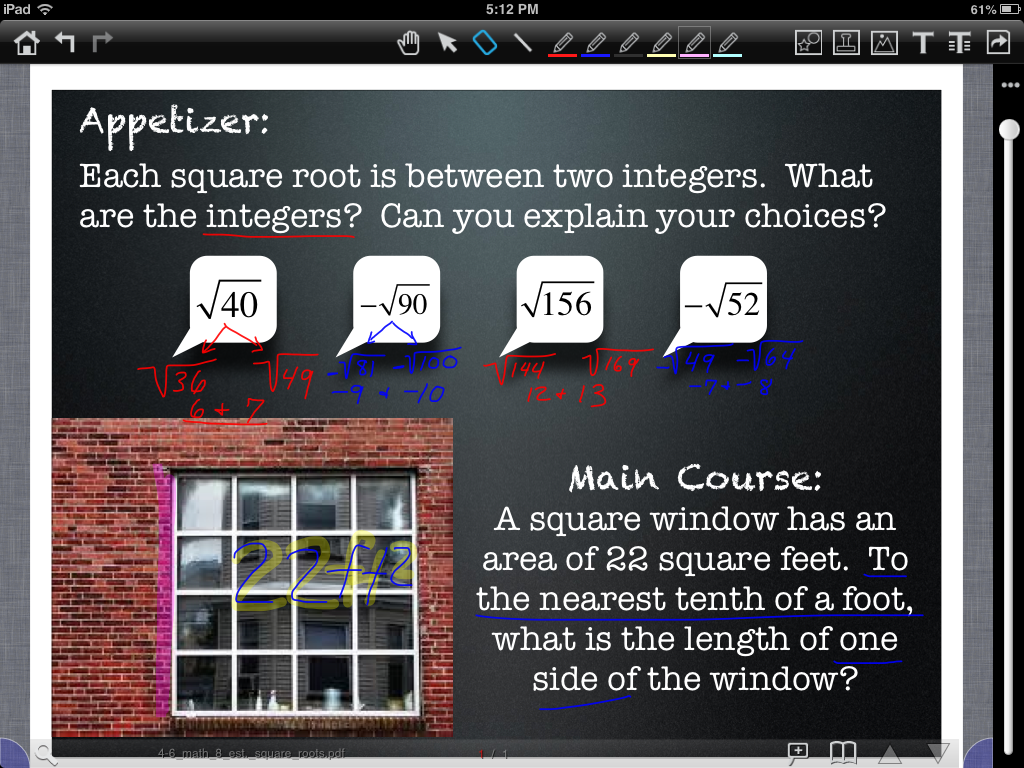
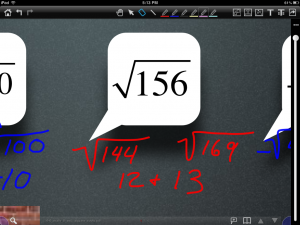
Another task we completed was a quick activity to get ready for slope-intercept form. The PDF simply said “Solve for y” and the students used DocAS to apply the algebra they knew to solve various linear functions for the variable “y”. Students especially enjoyed using what I call the “zoom box” feature in DocAS for this task. Basically, the app becomes a split-screen experience such that the top of the screen shows a “zoomed out” view, while the bottom portion of the screen becomes a “zoomed in” view of wherever one places the “zoom box”. This feature really helps make math work legible as well as appropriately sized. The incredible ability to zoom in and out on the iPad enables many things that paper never could.
 Students became somewhat competitive on the “beauty” of their work as well. Initial work was quite simple, but some took full advantage of the limitless color palate in the app and made their PDFs quite aesthetically pleasing. Students were eager to present solutions to the class, knowing how “pretty” their problems had become. I have no problem with students having a little bit of fun using colorful “ink” if the algebra is on track. And it was.
Students became somewhat competitive on the “beauty” of their work as well. Initial work was quite simple, but some took full advantage of the limitless color palate in the app and made their PDFs quite aesthetically pleasing. Students were eager to present solutions to the class, knowing how “pretty” their problems had become. I have no problem with students having a little bit of fun using colorful “ink” if the algebra is on track. And it was.
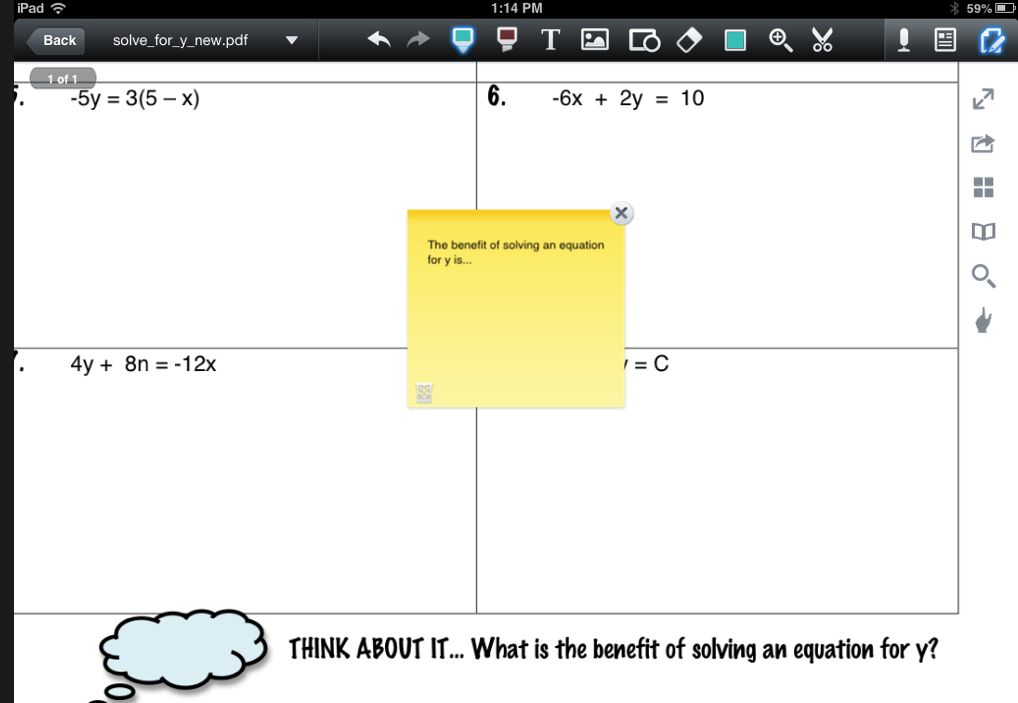
DocAS also has a nice “Stick Note” feature. At the bottom of the PDF, I posed the question, “What is the benefit of solving an equation for y?” As a paper copy, there literally would have been no room to answer this follow-up question. With a “Stick Note” in DocAS, we were able to answer this question… and put notes-to-self all over the place if needed! Simply go to the paper icon in the top right corner and choose “Stick Note” at the bottom of the list. Type needed notes, then close it up and it shrinks to an itty bitty call-out that can be moved anywhere in the document. Click on the mini call-out to see the note any time. The kids really liked this feature!

I don’t doubt that students may have initially commented about their distaste for “doing math” on the iPad. I wasn’t a fan of DocAS and expressed my distaste for it the first few times I tried using it. (A side note – it does lag a little, even now.) But a fantastic update and a little elbow grease have paid off. I feel more comfortable using the app, I understand many of the basic features and have been able to convey some of them to my students. Features I was unsure of… well, I just let a student guide us through what to do. I love learning from them when they have more experience with an app than I do. I am never alone. We are all learning. And as we learn and get beyond our first impressions of something new, sometimes we change our minds.


P.S. If you’d like a copy of the “Solve for y” sheet featured above, just zap this QR code:









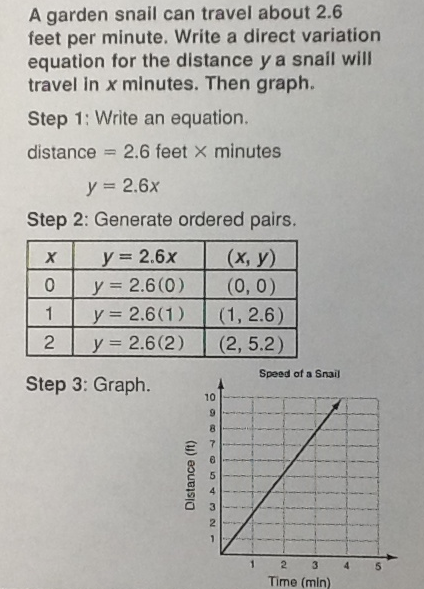





 Students became somewhat competitive on the “beauty” of their work as well. Initial work was quite simple, but some took full advantage of the limitless color palate in the app and made their PDFs quite aesthetically pleasing. Students were eager to present solutions to the class, knowing how “pretty” their problems had become. I have no problem with students having a little bit of fun using colorful “ink” if the algebra is on track. And it was.
Students became somewhat competitive on the “beauty” of their work as well. Initial work was quite simple, but some took full advantage of the limitless color palate in the app and made their PDFs quite aesthetically pleasing. Students were eager to present solutions to the class, knowing how “pretty” their problems had become. I have no problem with students having a little bit of fun using colorful “ink” if the algebra is on track. And it was.