While I’ve never fully implemented the “flipped classroom” idea with students, maybe I have done a few short-term “mini flips”. Many digital tools permit students to explore content at their own pace, and asynchronously, which can make “homework” an experience beyond handouts. Using tools like ThatQuiz, Desmos Activity Builder, or Nearpod to present content and pre-assess student knowledge informs my instructional planning from day to day (always helpful, but especially so at the start of a new school year). On the teacher side of the digital workflow, I’m able to gain insight to student mis/understandings as they’re working independently outside of class, so I know what I’m in for before our next class together.
While I’ve never fully implemented the “flipped classroom” idea with students, maybe I have done a few short-term “mini flips”. Many digital tools permit students to explore content at their own pace, and asynchronously, which can make “homework” an experience beyond handouts. Using tools like ThatQuiz, Desmos Activity Builder, or Nearpod to present content and pre-assess student knowledge informs my instructional planning from day to day (always helpful, but especially so at the start of a new school year). On the teacher side of the digital workflow, I’m able to gain insight to student mis/understandings as they’re working independently outside of class, so I know what I’m in for before our next class together.
In other words, I can see and analyze student work/thinking outside of class, either the evening I assigned the digital homework, or early the next morning as I review the report and sip my coffee! I get to “Anticipate” (Practice 1) before class, and even “Select” (Practice 3) and “Sequence” (Practice 4) authentic student work samples to focus on in class.
This may be a game-changer for some of you out there, as “Anticipating” can be quite challenging, can’t it? This is year 15 of teaching full-time for me, and just when I think I’ve seen every student error or misconception out there, someone comes up with something so awesomely and uniquely incorrect, I never *could* have anticipated it! With the digital tools we have today, when these unanticipated errors happen *outside* of class time and you get to see them before your next class meeting, you don’t have to feel (insert emotion here – however you feel when a kid does something uniquely wrong – are you excited about this mistake? Frustrated? Feeling like you need some time to analyze it more closely to see exactly what the kiddo is thinking?)
An example from my week was a Nearpod student-paced “homework” that was designed to start preparing Algebra students for TEKS A.5(A): Solve linear equations in one variable, including those for which the application of the distributive property is necessary and for which variables are included on both sides.
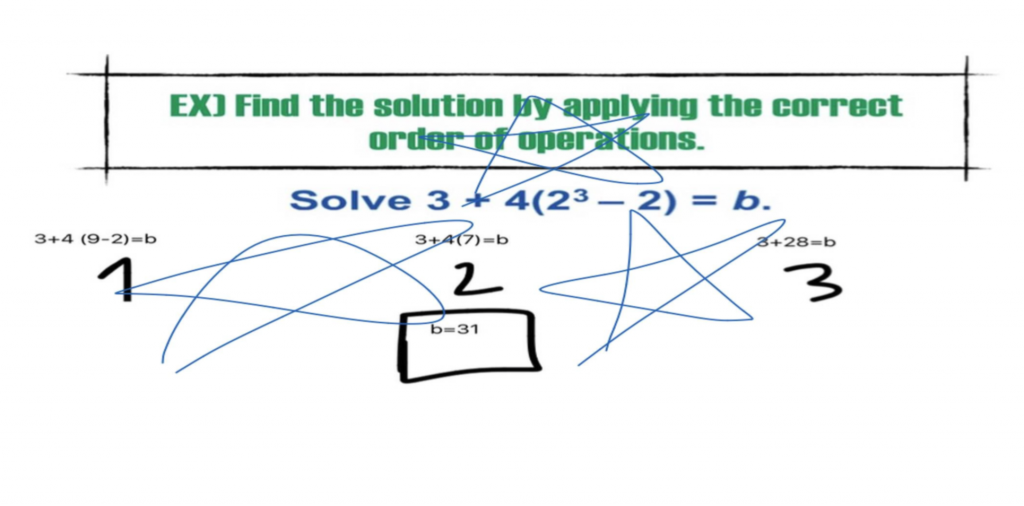
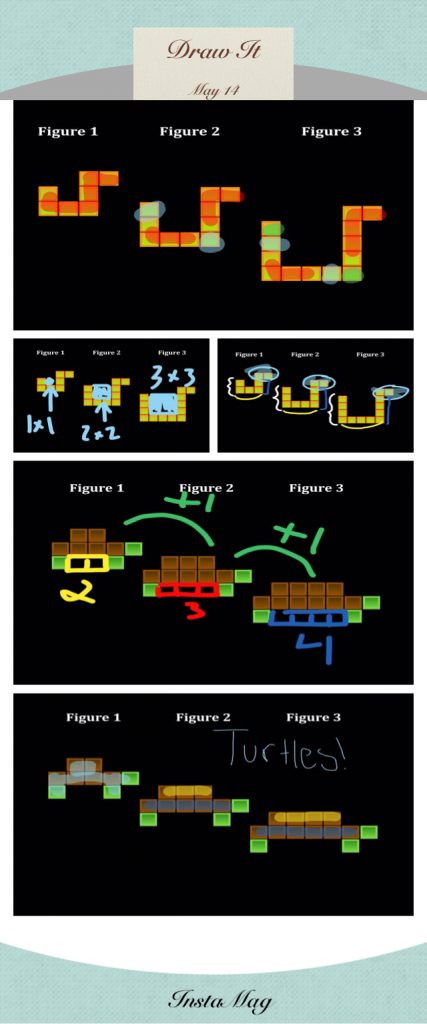
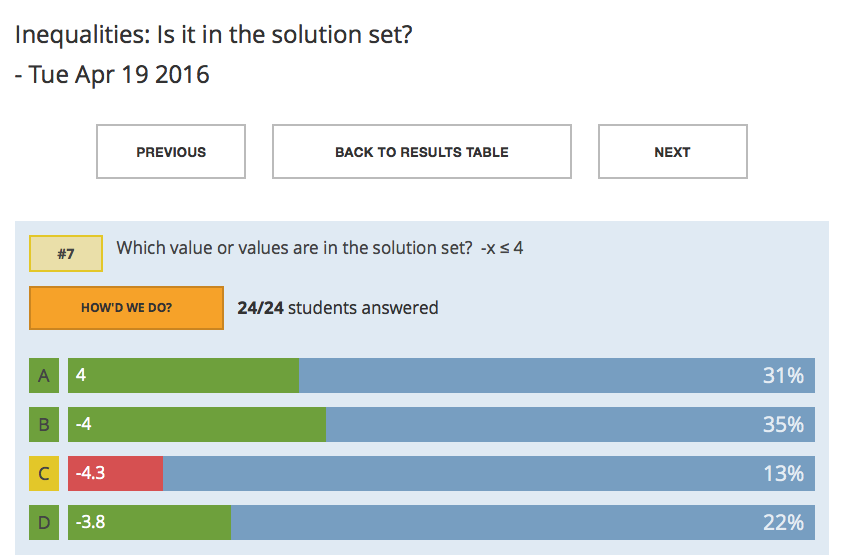
Students have an entire unit on equations coming up next, so in our first unit, we’ve been working on translating expressions, understanding the concept of equivalence, identifying and applying number properties, reviewing Order of Operations, and applying these ideas in problem-solving contexts. One day this past week, I assigned a self-paced Nearpod homework that asked students to use “Draw It” to solve and submit the solutions to various equations. As I viewed the Nearpod report, literally as I sipped my coffee the next morning, I took screenshots of/”selected” student work straight from the report, and dumped/”sequenced” these images into a new Nearpod. I added the anonymous student work samples as “backgrounds” to new “Draw It” slides so students would not only view the problems in class in a few short hours, but “Draw” on them to analyze them, “grade” them, and provide comments or feedback regarding errors. I figured I’d use this new Nearpod as our warm-up and homework follow-up.
It’s one thing to feature anonymous errors on the screen at the front of the class and talk about them, and how to fix them, together.
Through this experience, I learned it’s another thing entirely to ask *each* student to analyze the work and take a stand on its correctness or incorrectness.
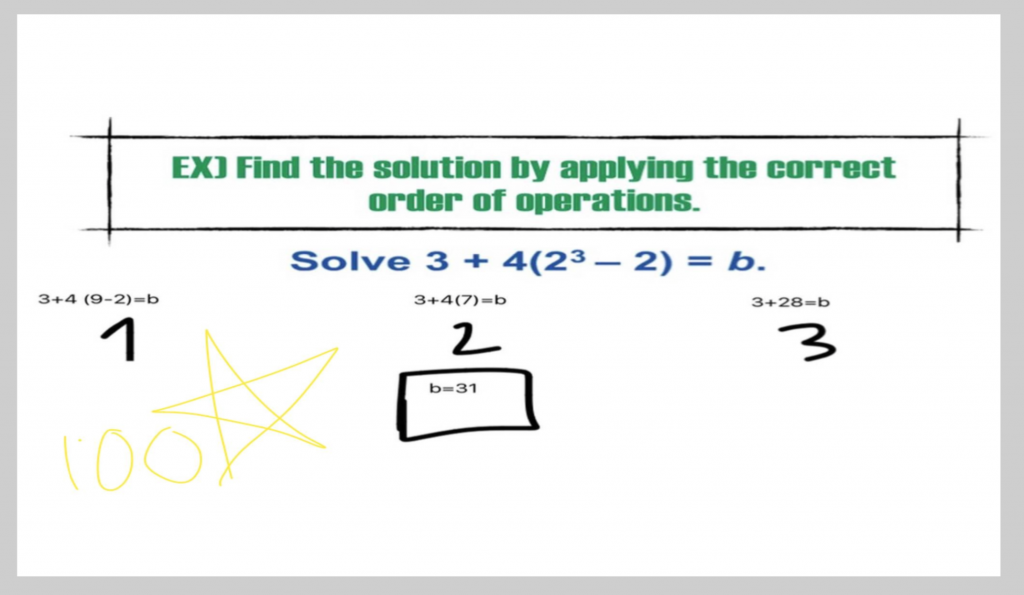
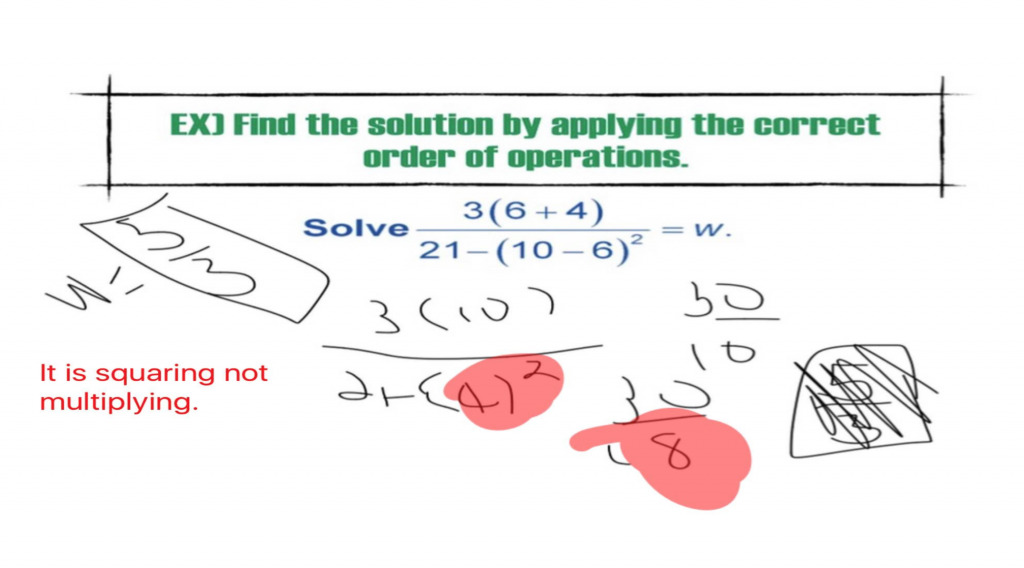
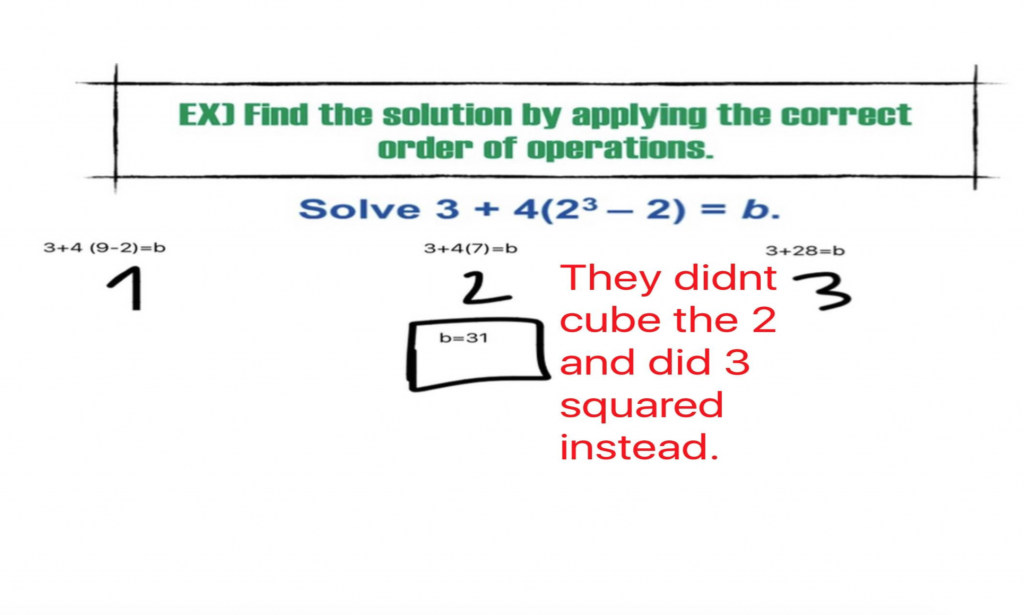
I didn’t tell students whether each work sample was “correct” or “incorrect” and it blew. my. mind. how quickly students looked at a problem and “drew” a star, or wrote a comment saying, “good job” when a problem was completely wrong! Wow! When every student is held accountable to take a stand on each problem, and literally document it…AND I’m able to showcase (anonymously) student comments on the work… well, it upped the ante and created a student-centered “Monitoring” experience (Practice 2) that made for a very interesting class!
Students who hastily marked an incorrect problem as “correct” quickly realized that they hadn’t truly analyzed the work of their peer. It was a healthy wake-up call, which helped students be more careful on the next problem.
Students realized that it’s very hard to provide feedback to an incorrect student who hasn’t shown much work. How can we help you if we really don’t understand your thought process because we can’t see it?
Sloppy work was not even considered. Students didn’t want to even *try* to analyze a peer’s thinking when it was difficult to follow. This created a kind of teacher empathy I could never have anticipated!
Students whose work samples were included in the Nearpod owned their work. They said, “This one is mine! I see now that I (insert self-analysis/explanation of error). How cool that we’re feeling safe enough in week 2 of school to own mistakes and correct them in front of the whole class?
All-in-all, I’ll be doing this digital-homework-goes-digital-for-discussion strategy again! In time, I hope to develop students who better analyze their own work as well as the work of others!
How do the “5 Practices” look in your classroom?
Bonus Resource: Here’s a Desmos Card Sort version of a popular Mathematics Assessment Project paper card sort. We used this as an extension activity in class. Enjoy!